
【题目】如图,在△ABC中,AB=AC,D为BC上一点(能与B重合,不与C重合),以DC为直径的半圆O,交AC于点E.
(1)如图1,若点D与点B重合,半圆交AB于点F,求证:AE=AF.
(2)设∠B=60°,若半圆与AB相切于点T,在图2中画出相应的图形,求∠AET的度数.
(3)设∠B=60°,BC=6,△ABC的外心为点P,若点P正好落在半圆与其直径组成的封闭图形的内部,直接写出DC的取值范围.

【答案】(1)证明见解析;(2)75°;(3)4<DC≤6.
【解析】
(1)连接BE,CF,根据已知条件,推断出△ABE≌△ACF即可;
(2)连接OT、OE、ET,根据已知推出∠OEC和∠TEO的度数,即可得出答案;
(3)以B为原点建立坐标系,求出各点坐标,设DC=a,写出圆O的解析式,再根据题意列出不等式计算即可.
证明:(1)如图1:连接BE,CF,

∵此时BC为直径,
∴∠BEC=∠CFB=90°,
∴∠AEB=∠AFC=90°,
又∵∠A=∠A,AB=AC,
∴△ABE≌△ACF,
∴AE=AF;
(2)如图2:连接OT、OE、ET,
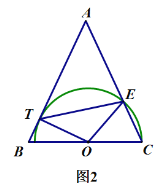
∵AB=AC,∠B=60°,
∴∠C=60°,
∵OE=OC,
∴∠EOC=∠OEC=60°,
∵AB是圆的切线,
∴OT⊥AB,
∵∠BOT=90°-60°=30°,
∴∠TOE=90°,
∵OT=OE,
∴∠TEO=45°,
∴∠AET=180°-45°-60°=75°;
(3)以B为原点建立坐标系,
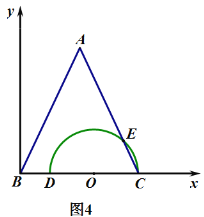
∵AB=AC,∠ABC=60°,
∴△ABC为正三角形,
∵BC=6,
∴C(6,0),A(3,![]() ),
),
∴△ABC的外心P(3,![]() ),
),
设DC=a,则圆O:![]() ,
,
当P在封闭图形的内部时,![]() ,
,
得a>4,
∴4<DC≤6.


科目:初中数学 来源: 题型:
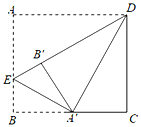
【题目】如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A′,折痕为DE.若将∠B沿EA′向内翻折,点B恰好落在DE上,记为B′,则AB=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
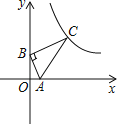
【题目】如图所示,点B的坐标为(0,4),点A是x正半轴上一点,点C在第一象限内,BC⊥AB于点B,∠OAB=∠BAC,当AC=10时,则过点C的反比例函数y=![]() 的比例系数k值为( )
的比例系数k值为( )
A.32 或 16B.48 或 64C.16 或 64D.32 或 80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
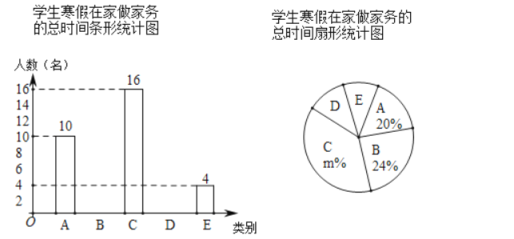
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-![]() (x-t)(x-t+6)与直线y=x-1有两个交点,这两个交点的纵坐标为m、n.双曲线y=
(x-t)(x-t+6)与直线y=x-1有两个交点,这两个交点的纵坐标为m、n.双曲线y=![]() 的两个分支分别位于第二、四象限,则t的取值范围是( )
的两个分支分别位于第二、四象限,则t的取值范围是( )
A.t<0B.0<t<6C.1<t<7D.t<1或t>6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定宇(依次记为![]() ).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上
).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上![]() 四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.
四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.

(1)班长在四种卡片中随机抽到标号为![]() 的概率为_______.
的概率为_______.
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO,则图中阴影部分的面积之和为( )
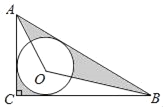
A.10﹣![]() B.14﹣
B.14﹣![]() πC.12D.14
πC.12D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.
已知:线段![]() .求作:等腰
.求作:等腰![]() ,使
,使![]() ,
,![]() 边上的高为
边上的高为![]() .作法:如图,(1)作线段
.作法:如图,(1)作线段![]() ;(2)作线段
;(2)作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ;(3)在射线
;(3)在射线![]() 上顺次截取线段
上顺次截取线段![]() ,连接
,连接![]() .所以
.所以![]() 即为所求作的等腰三角形.
即为所求作的等腰三角形.
请回答:得到![]() 是等腰三角形的依据是:
是等腰三角形的依据是:
①_____:
②_____.
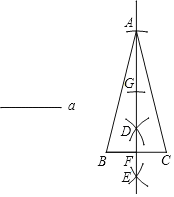
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与y轴交于点C,连接AC,BC,将
,与y轴交于点C,连接AC,BC,将![]() 沿BC所在的直线翻折,得到
沿BC所在的直线翻折,得到![]() ,连接OD.
,连接OD.
(1)用含a的代数式表示点C的坐标.
(2)如图1,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3)设![]() 的面积为S1,
的面积为S1,![]() 的面积为S2,若
的面积为S2,若![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com