
【题目】如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
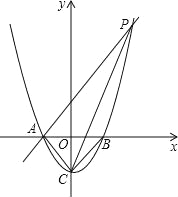
(1)求A、B、C三点的坐标;
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存在,请求出M点的坐标;否则,请说明理由.
【答案】(1)A(-1,0),B(1,0),C(0,-1);(2)4;(3)M点的坐标为(-2,3),(![]() ,
,![]() ),(4,15).
),(4,15).
【解析】
试题分析:(1)抛物线与x轴的交点,即当y=0,C点坐标即当x=0,分别令y以及x为0求出A,B,C坐标的值;
(2)四边形ACBP的面积=△ABC+△ABP,由A,B,C三点的坐标,可知△ABC是直角三角形,且AC=BC,则可求出△ABC的面积,根据已知可求出P点坐标,可知点P到直线AB的距离,从而求出△ABP的面积,则就求出四边形ACBP的面积;
(3)假设存在这样的点M,两个三角形相似,根据题意以及上两题可知,∠PAC和∠MGA是直角,只需证明![]() 或
或![]() 即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.
即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.
试题解析:(1)令y=0,
得x2-1=0
解得x=±1,
令x=0,得y=-1
∴A(-1,0),B(1,0),C(0,-1);
(2)∵OA=OB=OC=1,
∴∠BAC=∠ACO=∠BCO=∠CBO=45°.
∵AP∥CB,
∴∠PAB=∠CBO=45°.
过点P作PE⊥x轴于E,则△APE为等腰直角三角形,
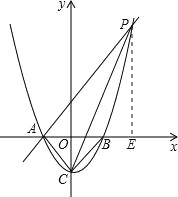
令OE=a,则PE=a+1,
∴P(a,a+1).
∵点P在抛物线y=x2-1上,
∴a+1=a2-1.
解得a1=2,a2=-1(不合题意,舍去).
∴PE=3.
∴四边形ACBP的面积S=![]() ABOC+
ABOC+![]() ABPE=
ABPE=![]() ×2×1+
×2×1+![]() ×2×3=4;
×2×3=4;
(3)假设存在
∵∠PAB=∠BAC=45°,
∴PA⊥AC
∵MG⊥x轴于点G,
∴∠MGA=∠PAC=90°
在Rt△AOC中,OA=OC=1,
∴AC=![]()
在Rt△PAE中,AE=PE=3,
∴AP=3![]()
设M点的横坐标为m,则M(m,m2-1)
①点M在y轴左侧时,则m<-1.
(ⅰ)当△AMG∽△PCA时,有![]() .
.
∵AG=-m-1,MG=m2-1.
即![]()
解得m1=-1(舍去)m2=![]() (舍去).
(舍去).
(ⅱ)当△MAG∽△PCA时有![]() ,
,
即![]() .
.
解得:m=-1(舍去)m2=-2.
∴M(-2,3).
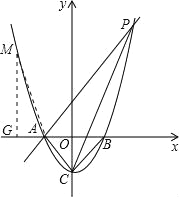
②点M在y轴右侧时,则m>1
(ⅰ)当△AMG∽△PCA时有![]()
∵AG=m+1,MG=m2-1
∴![]()
解得m1=-1(舍去)m2=![]() .
.
∴M(![]() ,
,![]() ).
).
(ⅱ)当△MAG∽△PCA时有![]() ,
,
即![]() .
.
解得:m1=-1(舍去)m2=4,
∴M(4,15).
∴存在点M,使以A、M、G三点为顶点的三角形与△PCA相似
M点的坐标为(-2,3),(![]() ,
,![]() ),(4,15).
),(4,15).



科目:初中数学 来源: 题型:
【题目】“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定宇(依次记为![]() ).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上
).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上![]() 四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.
四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.

(1)班长在四种卡片中随机抽到标号为![]() 的概率为_______.
的概率为_______.
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
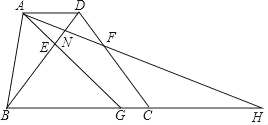
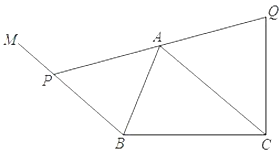
【题目】如图,在梯形ABCD中,AD∥BC,BC=18,DB=DC=15,点E、F分别在线段BD、CD上,DE=DF=5.AE的延长线交边BC于点G,AF交BD于点N、其延长线交BC的延长线于点H.
(1)求证:BG=CH;
(2)设AD=x,△ADN的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)联结FG,当△HFG与△ADN相似时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .过点
.过点![]() 作
作![]() ,动点
,动点![]() 在射线
在射线![]() 上(点
上(点![]() 不与
不与![]() 重合),联结
重合),联结![]() 并延长到点
并延长到点![]() ,使
,使![]() .
.
(1)求![]() 的面积;
的面积;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
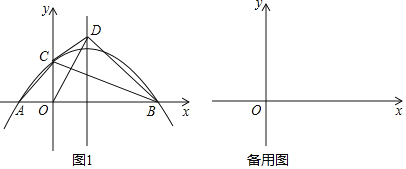
【题目】在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与y轴交于点C,连接AC,BC,将
,与y轴交于点C,连接AC,BC,将![]() 沿BC所在的直线翻折,得到
沿BC所在的直线翻折,得到![]() ,连接OD.
,连接OD.
(1)用含a的代数式表示点C的坐标.
(2)如图1,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3)设![]() 的面积为S1,
的面积为S1,![]() 的面积为S2,若
的面积为S2,若![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区检票口有A、B、C、D共4个检票通道.甲、乙两人到该景区游玩,两人分别从4个检票通道中随机选择一个检票.
(1)甲选择A检票通道的概率是 ;
(2)求甲乙两人选择的检票通道恰好相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
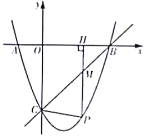
【题目】如图,若抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上一动点,过点
下方抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
①线段![]() 是否有最大值?如果有,求出最大值;如果没有,请说明理由;
是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,恰好使
,恰好使![]() 是以
是以![]() 为腰的等腰三角形?如果存在,请直接写出点
为腰的等腰三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店3月份购进甲种水果50千克、乙种水果80千克,共花费1700元,其中甲种水果以15元/千克,乙种水果以20元/千克全部售出;4月份又以同样的价格购进甲种水果60千克、乙种水果40千克,共花费1200元,由于市场不景气,4月份两种水果均以3月份售价的8折全部售出.
(1)求甲、乙两种水果的进价每千克分别是多少元?
(2)请计算该水果店3月和4月甲、乙两种水果总赢利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com