
【题目】抛物线![]() (
(![]() 是常数),
是常数),![]() ,顶点坐标为
,顶点坐标为![]() .给出下列结论:①若点
.给出下列结论:①若点![]() 与点
与点![]() 在该抛物线上,当
在该抛物线上,当![]() 时,则
时,则![]() ;②关于
;②关于![]() 的一元二次方程
的一元二次方程![]() 无实数解,那么( )
无实数解,那么( )
A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误
【答案】A
【解析】
①根据二次函数的增减性进行判断便可;
②先把顶点坐标代入抛物线的解析式,求得m,再把m代入一元二次方程ax2-bx+c-m+1=0的根的判别式中计算,判断其正负便可判断正误.
解:①∵顶点坐标为![]() ,
,![]()
∴点(n,y1)关于抛物线的对称轴x=![]() 的对称点为(1-n,y1),
的对称点为(1-n,y1),
∴点(1-n,y1)与![]() 在该抛物线的对称轴的右侧图像上,
在该抛物线的对称轴的右侧图像上,
![]()
![]()
∵a>0,
∴当x>![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
∴y1<y2,故此小题结论正确;
②把![]() 代入y=ax2+bx+c中,得
代入y=ax2+bx+c中,得![]() ,
,
∴一元二次方程ax2-bx+c-m+1=0中,
△=b2-4ac+4am-4a![]()
∴一元二次方程ax2-bx+c-m+1=0无实数解,故此小题正确;
故选A.


科目:初中数学 来源: 题型:
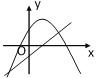
【题目】如图,抛物线y=-![]() (x-t)(x-t+6)与直线y=x-1有两个交点,这两个交点的纵坐标为m、n.双曲线y=
(x-t)(x-t+6)与直线y=x-1有两个交点,这两个交点的纵坐标为m、n.双曲线y=![]() 的两个分支分别位于第二、四象限,则t的取值范围是( )
的两个分支分别位于第二、四象限,则t的取值范围是( )
A.t<0B.0<t<6C.1<t<7D.t<1或t>6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),对称轴与
的左侧),对称轴与![]() 轴交于点(3,0),且
轴交于点(3,0),且![]() .
.
(1)求抛物线![]() 的表达式及顶点坐标;
的表达式及顶点坐标;
(2)将抛物线![]() 平移,得到的新抛物线
平移,得到的新抛物线![]() 的顶点为(0,﹣1),抛物线
的顶点为(0,﹣1),抛物线![]() 的对称轴与两条抛物线
的对称轴与两条抛物线![]() ,
,![]() 围成的封闭图形为
围成的封闭图形为![]() .直线
.直线![]() 经过点
经过点![]() .若直线
.若直线![]() 与图形
与图形![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
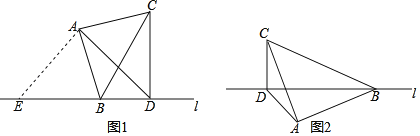
【题目】如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.
(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为 °,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为 ;
(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;
(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
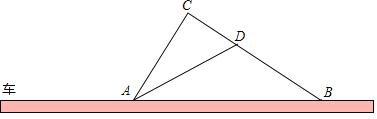
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
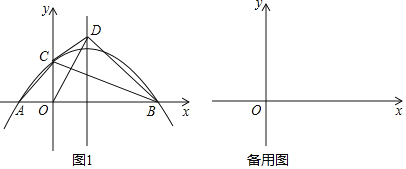
【题目】在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与y轴交于点C,连接AC,BC,将
,与y轴交于点C,连接AC,BC,将![]() 沿BC所在的直线翻折,得到
沿BC所在的直线翻折,得到![]() ,连接OD.
,连接OD.
(1)用含a的代数式表示点C的坐标.
(2)如图1,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3)设![]() 的面积为S1,
的面积为S1,![]() 的面积为S2,若
的面积为S2,若![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
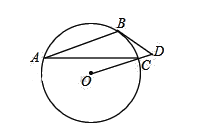
【题目】已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径等于4,tan∠ACB=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受新型冠状病毒肺炎影响,学校开学时间延迟,为了保证学生停课不停学,某校开始实施网上教学,张老师统计了本班学生一周网上上课的时间(单位:分钟)如下:200,180,150,200,250.关于这组数据,下列说法正确的是( )
A.中位数是200B.众数是150C.平均数是190D.方差为0
查看答案和解析>>
科目:初中数学 来源: 题型:
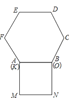
【题目】已知正方形![]() 和正六边形
和正六边形![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转;再绕点
边重合,完成第一次旋转;再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点
经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点![]() ,
,![]() 之间距离的最大值是______.
之间距离的最大值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com