
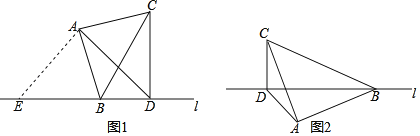
【题目】如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.
(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为 °,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为 ;
(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;
(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.
【答案】(1)45°,CD+DB=![]() AD;(2)线段AD,BD,CD的数量关系会变化,数量关系为BD﹣CD=
AD;(2)线段AD,BD,CD的数量关系会变化,数量关系为BD﹣CD=![]() AD.证明见解析;(3)1+
AD.证明见解析;(3)1+![]() .
.
【解析】
(1)由∠BAC=90°,且AB=AC,可得∠ACB=∠ABC=45°,由∠BAC=∠BDC=90°,推出A、B、C、D四点共圆,所以∠ADB=∠ACB=45°;由题意知△EAB≌△DAC,所以BE=CD,由AE=AD,∠EAD=90°,可知△ADE是等腰直角三角形,推出CD+DB=EB+BD=DE=![]() AD;
AD;
(2)如图2,将AD绕点A顺时针旋转90°交直线l于点E.易证△EAB≌△DAC(SAS),则BE=CD,由AE=AD,∠EAD=90°,所以△ADE是等腰直角三角形,则DE=![]() AD,由BDCD=BDBE=DE,推出BDCD=
AD,由BDCD=BDBE=DE,推出BDCD=![]() AD;
AD;
(3)当点D在线段AB的垂直平分线上且在AB的左侧时,△ABD的面积最大,据此即可求解.
解:(1)①如图,在图1中.
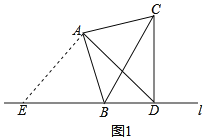
∵∠BAC=90°,且AB=AC,
∴∠ACB=∠ABC=45°,
∵∠BAC=∠BDC=90°,
∴A、B、C、D四点共圆,
∴∠ADB=∠ACB=45°;
②由题意可知,∠EAD=∠BAC=90°,
∴∠EAB=∠DAC,
又AE=AD,AB=AC,
∴△EAB≌△DAC(SAS),
∴BE=CD,
∵AE=AD,∠EAD=90°,
∴△ADE是等腰直角三角形,
∴DE=![]() =
=![]() AD,
AD,
∵CD+DB=EB+BD=DE,
∴CD+DB=![]() AD;
AD;
故答案为45°;CD+DB=![]() AD;
AD;
(2)线段AD,BD,CD的数量关系会变化,数量关系为BD﹣CD=![]() A.
A.
理由如下:
如图2,将AD绕点A顺时针旋转90°交直线l于点E.
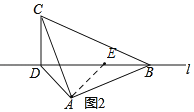
则∠DAE=∠CAB=90°,
∴∠DAC=∠EAB,
又AD=AE,AC=AB,
∴△EAB≌△DAC(SAS),
∴BE=CD,
∵AE=AD,∠EAD=90°,
∴△ADE是等腰直角三角形,
∴DE=![]() =
=![]() AD,
AD,
∵BD﹣CD=BD﹣BE=DE,
∴BD﹣CD=![]() AD;
AD;
(3)由(2)知,△CDA≌△BEA,
∴∠CDA=∠AEB,
∵∠DEA=45°,
∴∠AEB=180°﹣45°=135°,
∴∠CDA=∠AEB=135°,
∴∠CDA+∠ABC=135°+45°=180°,
∴A、B、C、D四点共圆,
于是作A、B、C、D外接圆⊙O,如图3.
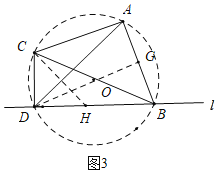
当点D在线段AB的垂直平分线上且在AB的左侧时,△ABD的面积最大.
作DG⊥AB,则DG平分∠ADB,DB=DA,在DA上截取一点H,使得CD=DH=1,
∵∠ADB=∠ACB=45°,
∴∠GDB=22.5°,∠DBG=67.5°,
∴∠DBC=67.5°﹣45°=22.5°,
∠HCB=∠DHC﹣∠HBC=45°﹣22.5°=22.5°,
∴∠HCB=∠HBC,
∴HB=CH=![]() =
=![]() ,
,
∴AD=BD=DH+BH=1+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
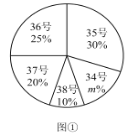
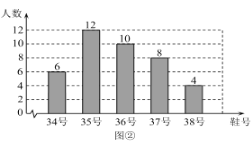
(Ⅰ)本次接受随机抽样调查的学生人数为________,图①中![]() 的值为________;
的值为________;
(Ⅱ)求本次调查获取的样本数据的众数和中位数;
(Ⅲ)根据样本数据,若学校计划购买150双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
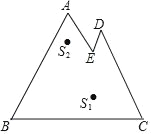
【题目】对于封闭的平面图形,如果图形上或图形内的点S到图形上的任意一点P之间的线段都在图形内或图形上,那么这样的点S称为“亮点”.如图,对于封闭图形ABCDE,S1是“亮点”,S2不是“亮点”,如果AB∥DE,AE∥DC,AB=2,AE=1,∠B=∠C=60°,那么该图形中所有“亮点”组成的图形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )
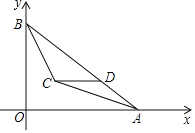
A.( ![]() ,2)B.(
,2)B.( ![]() ,1)C.(
,1)C.( ![]() ,2)D.(
,2)D.(![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前,商丘市正在围绕打响“游商丘古都城,读华夏文明史”文化旅游品牌,加快推进商丘景点保护性修复与宣传工作,以此带动以文化为核心的全域旅游跨越发展,打造华夏历史文明商丘传承创新区.随着社会经济的发展和城市周边交通状况的改善,旅游已成为人们的一种生活时尚,某中学开展以“我最喜欢的商丘风景区”为主题的调查活动,围绕“在森林公园、日月湖、汉梁公园和睢阳古城”四个风景区中,你最喜欢哪一个?(必选且只选一个)”的问题,在全校范围内随机抽取了部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
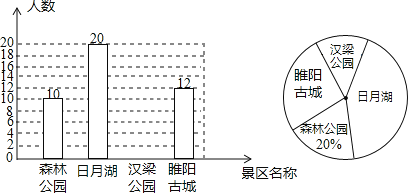
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若该中学共有3000名学生,请你估计最喜欢日月湖风景区的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 是常数),
是常数),![]() ,顶点坐标为
,顶点坐标为![]() .给出下列结论:①若点
.给出下列结论:①若点![]() 与点
与点![]() 在该抛物线上,当
在该抛物线上,当![]() 时,则
时,则![]() ;②关于
;②关于![]() 的一元二次方程
的一元二次方程![]() 无实数解,那么( )
无实数解,那么( )
A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误
查看答案和解析>>
科目:初中数学 来源: 题型:
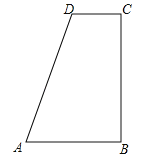
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小聪参加了![]() 跑的5期集训,每期集训结束市进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图:
跑的5期集训,每期集训结束市进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图:
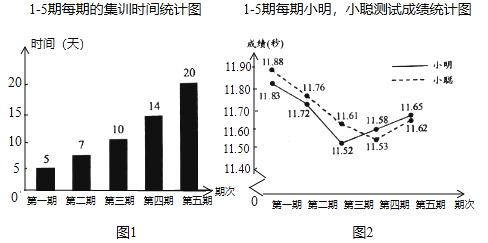
根据图中信息,解答下列问题:
(1)这5期的集训共有多少天?小聪5次测试的平均成绩是多少?
(2)根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,说说你的想法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com