
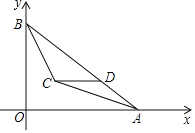
【题目】如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )
A.( ![]() ,2)B.(
,2)B.( ![]() ,1)C.(
,1)C.( ![]() ,2)D.(
,2)D.(![]() ,1)
,1)
【答案】A
【解析】
延长DC交y轴于F,过C作CG⊥OA于G,CE⊥AB于E,根据角平分线的性质得到FC=CG=CE,求得DH=CG=CF,设DH=3x,AH=4x,根据勾股定理得到AD=5x,根据平行线的性质得到∠DCA=∠CAG,求得∠DCA=∠DAC,得到CD=HG=AD=5x,列方程即可得到结论.
解:延长DC交y轴于F,过C作CG⊥OA于G,CE⊥AB于E,
∵CD∥x轴,
∴DF⊥OB,
∵∠BAO,∠ABO的平分线相交于点C,
∴FC=CG=CE,
∴DH=CG=CF,
∵A(8,0),B(0,6),
∴OA=8,OB=6,
∴tan∠OAB=![]() =
=![]() =
=![]() ,
,
∴设DH=3x,AH=4x,
∴AD=5x,
∵CD∥OA,
∴∠DCA=∠CAG,
∵∠DAC=∠GAC,
∴∠DCA=∠DAC,
∴CD=HG=AD=5x,
∴3x+5x+4x=8,
∴x=![]() ,
,
∴DH=2,OH=![]() ,
,
∴D(![]() ,2),
,2),
故选:A.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
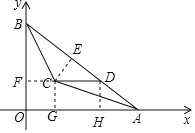
【题目】网络时代,新兴词汇层出不穷.为了解大众对网络词汇的理解,某兴趣小组举行了一个“我是路人甲”的调查活动:选取四个热词A:“硬核人生”,B:“好嗨哦”,C:“双击666”,D:“杠精时代”在街道上对流动人群进行了抽样调查,要求被调查的每位只能勾选一个最熟悉的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名路人.
(2)补全条形统计图;
(3)扇形图中的b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
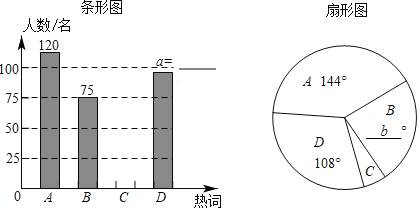
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),对称轴与
的左侧),对称轴与![]() 轴交于点(3,0),且
轴交于点(3,0),且![]() .
.
(1)求抛物线![]() 的表达式及顶点坐标;
的表达式及顶点坐标;
(2)将抛物线![]() 平移,得到的新抛物线
平移,得到的新抛物线![]() 的顶点为(0,﹣1),抛物线
的顶点为(0,﹣1),抛物线![]() 的对称轴与两条抛物线
的对称轴与两条抛物线![]() ,
,![]() 围成的封闭图形为
围成的封闭图形为![]() .直线
.直线![]() 经过点
经过点![]() .若直线
.若直线![]() 与图形
与图形![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
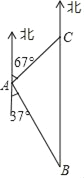
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
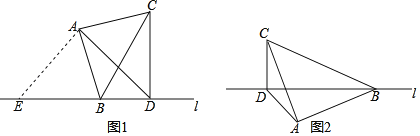
【题目】如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.
(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为 °,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为 ;
(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;
(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
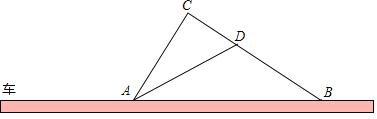
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
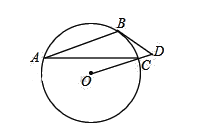
【题目】已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径等于4,tan∠ACB=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴正半轴交于点
轴正半轴交于点![]() ,
,![]() .
.
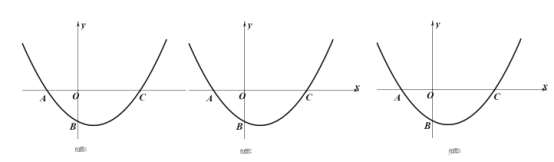
(1)如图1,求![]() 的值;
的值;
(2)如图2,抛物线的顶点坐标是![]() ,点
,点![]() 是第一象限抛物线上的一点,连接
是第一象限抛物线上的一点,连接![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,设点
,设点![]() 的横坐标是
的横坐标是![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如图3,在(2)的条件下,当![]() 时,过点
时,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,点
,点![]() 是
是![]() 轴下方抛物线上的一个动点,连接
轴下方抛物线上的一个动点,连接![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com