
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),对称轴与
的左侧),对称轴与![]() 轴交于点(3,0),且
轴交于点(3,0),且![]() .
.
(1)求抛物线![]() 的表达式及顶点坐标;
的表达式及顶点坐标;
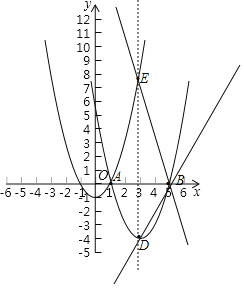
(2)将抛物线![]() 平移,得到的新抛物线
平移,得到的新抛物线![]() 的顶点为(0,﹣1),抛物线
的顶点为(0,﹣1),抛物线![]() 的对称轴与两条抛物线
的对称轴与两条抛物线![]() ,
,![]() 围成的封闭图形为
围成的封闭图形为![]() .直线
.直线![]() 经过点
经过点![]() .若直线
.若直线![]() 与图形
与图形![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)抛物线![]() 的表达式为
的表达式为![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ;(2)
;(2)![]() 的取值范围是
的取值范围是![]() 且
且![]() .
.
【解析】
(1)利用对称轴与x轴交于点(3,0),AB=4,可得A、B坐标,将A、B坐标代入![]() 可得解析式,化成顶点式求得抛物线顶点坐标;
可得解析式,化成顶点式求得抛物线顶点坐标;
(2)利用平移后的![]() 的顶点为(0,﹣1)可得抛物线C2的解析式,易得抛物线
的顶点为(0,﹣1)可得抛物线C2的解析式,易得抛物线![]() 的对称轴
的对称轴![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]() ,当直线
,当直线![]() 过点
过点![]() 和点
和点![]() 时,代入
时,代入![]() 可得
可得![]() ,将
,将![]() 和点
和点![]() 代入
代入![]() 可得
可得![]() ,易得k的取值范围.
,易得k的取值范围.
(1)∵抛物线![]() 的对称轴与
的对称轴与![]() 轴交于点(3,0),
轴交于点(3,0),
∴抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]()
解得![]()
∴抛物线![]() 的表达式为
的表达式为![]() .
.
即![]() .
.
∴抛物线![]() 的顶点为
的顶点为![]() .
.
(2)∵平移后得到的新抛物线![]() 的顶点为
的顶点为![]() ,
,
∴抛物线![]() 的表达式为
的表达式为![]() .
.
∴抛物线![]() 的对称轴
的对称轴![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]()
①当直线![]() 过点
过点![]() 和点
和点![]() 时,
时,
得![]()
解得![]() .
.
②当直线![]() 过点
过点![]() 和点
和点![]() 时,
时,
得![]()
解得![]()
∴结合函数图象可知,![]() 的取值范围是
的取值范围是![]() 且
且![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
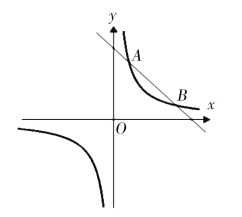
【题目】如图,双曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,点P是x轴上一动点.
,点P是x轴上一动点.
(1)求双曲线![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)当![]() 时,直接写出x的取值范围;
时,直接写出x的取值范围;
(3)当![]() 是等腰三角形时,求点P的坐标.
是等腰三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一种优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)满足的关系为一次函数
(元/千克)满足的关系为一次函数![]() .
.
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量;
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
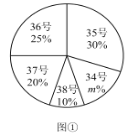
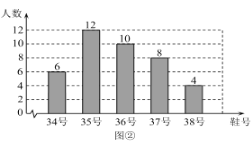
(Ⅰ)本次接受随机抽样调查的学生人数为________,图①中![]() 的值为________;
的值为________;
(Ⅱ)求本次调查获取的样本数据的众数和中位数;
(Ⅲ)根据样本数据,若学校计划购买150双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于封闭的平面图形,如果图形上或图形内的点S到图形上的任意一点P之间的线段都在图形内或图形上,那么这样的点S称为“亮点”.如图,对于封闭图形ABCDE,S1是“亮点”,S2不是“亮点”,如果AB∥DE,AE∥DC,AB=2,AE=1,∠B=∠C=60°,那么该图形中所有“亮点”组成的图形的面积为_____.
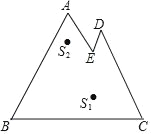
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )
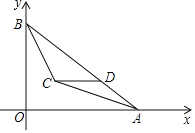
A.( ![]() ,2)B.(
,2)B.( ![]() ,1)C.(
,1)C.( ![]() ,2)D.(
,2)D.(![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 是常数),
是常数),![]() ,顶点坐标为
,顶点坐标为![]() .给出下列结论:①若点
.给出下列结论:①若点![]() 与点
与点![]() 在该抛物线上,当
在该抛物线上,当![]() 时,则
时,则![]() ;②关于
;②关于![]() 的一元二次方程
的一元二次方程![]() 无实数解,那么( )
无实数解,那么( )
A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选好志愿者,支持军运会.武汉市某校团委组织了一次八年级600名学生参加的“武汉军运知多少”知识大赛.为了了解本次大赛的成绩,随机抽取了部分学生的成绩作为样本,按A,B,C,D四个等级进行统计,制成如下不完整的统计图.(说明:A级80分- 100分,B级70分-79分,C级60-69分,D级0分-59分)
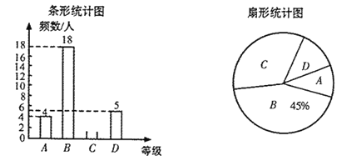
根据所给信息,解答以下问题:
(1)在扇形统计图中,C级对应的扇形的圆心角是_______度;
(2)直接写出条形统计图B级的頻数_______;
(3)所抽取学生的足球运球测试成绩的中位数会落在_______等级;
(4)若成绩达到A级的学生可以选为志愿者,请估计该校八年级600名学生中可以选为志愿者学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com