
【题目】已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足∠D=∠ACB.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径等于4,tan∠ACB=![]() ,求CD的长.
,求CD的长.
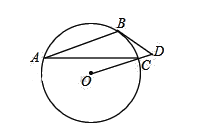
【答案】(1)详见解析;(2)CD=1
【解析】
(1)相切,连接OB,通过平行线、弦切角定理、等边对等角,得出相等的角,然后将这些相等的角进行置换,最终转换到一个三角形中,根据三角形的内角和来求出度数,从而得出∠OBD=90°.
(2)先求得∠D的正切值,在直角三角形OBD中,有半径的长和∠D的正切值,可用正弦函数求出OD的长,从而求出CD的长.
(1)直线BD与⊙O相切.
证明:如图,连接OB.
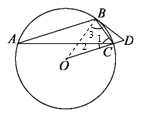
∵∠OCB=∠CBD+∠D,∠1=∠D,
∴∠2=∠CBD,
∵AB∥OC,
∴∠2=∠A,
∴∠A=∠CBD.
∵OB=OC,
∴∠BOC+2∠3=180°.
∵∠BOC=2∠A,
∴∠A+∠3=90°.
∴∠CBD+∠3=90°.
∴∠OBD=90°.
∴直线BD与⊙O相切.
(2)∵∠D=∠ACB,tan∠ACB=![]() ,
,
∴tan∠D=![]() .
.
∵∠OBD=90°,OB=4,tan∠D=![]() ,
,
∴![]() ,
,
∴CD=OD-OC=1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一种优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)满足的关系为一次函数
(元/千克)满足的关系为一次函数![]() .
.
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量;
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
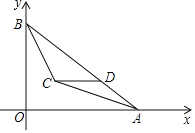
【题目】如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )
A.( ![]() ,2)B.(
,2)B.( ![]() ,1)C.(
,1)C.( ![]() ,2)D.(
,2)D.(![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 是常数),
是常数),![]() ,顶点坐标为
,顶点坐标为![]() .给出下列结论:①若点
.给出下列结论:①若点![]() 与点
与点![]() 在该抛物线上,当
在该抛物线上,当![]() 时,则
时,则![]() ;②关于
;②关于![]() 的一元二次方程
的一元二次方程![]() 无实数解,那么( )
无实数解,那么( )
A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误
查看答案和解析>>
科目:初中数学 来源: 题型:
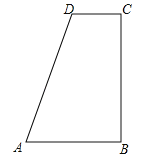
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
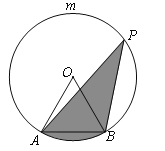
【题目】如图,AB是⊙O的弦,AB=4,点P在![]() 上运动(点P不与点A、B重合),且∠APB=30°,设图中阴影部分的面积为y.
上运动(点P不与点A、B重合),且∠APB=30°,设图中阴影部分的面积为y.
(1)⊙O的半径为 ;
(2)若点P到直线AB的距离为x,求y关于x的函数表达式,并直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选好志愿者,支持军运会.武汉市某校团委组织了一次八年级600名学生参加的“武汉军运知多少”知识大赛.为了了解本次大赛的成绩,随机抽取了部分学生的成绩作为样本,按A,B,C,D四个等级进行统计,制成如下不完整的统计图.(说明:A级80分- 100分,B级70分-79分,C级60-69分,D级0分-59分)
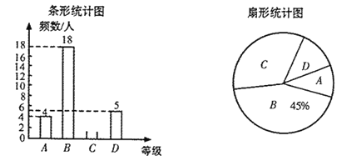
根据所给信息,解答以下问题:
(1)在扇形统计图中,C级对应的扇形的圆心角是_______度;
(2)直接写出条形统计图B级的頻数_______;
(3)所抽取学生的足球运球测试成绩的中位数会落在_______等级;
(4)若成绩达到A级的学生可以选为志愿者,请估计该校八年级600名学生中可以选为志愿者学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过
经过![]() 、
、![]() 两点.
两点.
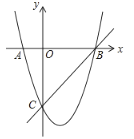
(1)求抛物线的解析式;
(2)过点![]() 作直线
作直线![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com