
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P是第一象限角平分线上的一点,OP=![]() ,直角三角板的直角顶点与点P重合,把直角三角板绕点P转动,另两条直角边所在直线与x轴正半轴、y轴正半轴分别交于A、B两点
,直角三角板的直角顶点与点P重合,把直角三角板绕点P转动,另两条直角边所在直线与x轴正半轴、y轴正半轴分别交于A、B两点

(1)求点P的坐标
(2)若点A的坐标为(0,m),点B的坐标为(n,0),试判断m、n有什么数量关系,并说明理由
(3)连接AB,△ABO的面积是否存在最大值,若存在,求出最大值,若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题探究
①如图1,在直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,则
,则![]() 的最小值为_________.
的最小值为_________.
②如图2,在等腰直角![]() 中,
中,![]() ,若
,若![]() ,求边
,求边![]() 的长度(用含
的长度(用含![]() 的代数式表示);
的代数式表示);
(2)问题解决
③如图3,在等腰直角![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,若点
的中点,若点![]() 是
是![]() 边上一点,试求
边上一点,试求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
如图在等边三角形ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边三角形CDE,连接BE.

(1)填空:∠CAM= ;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,
①当点D在线段AM上时,求∠AOB的度数;
②当动点D在直线AM上时,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断CD与圆O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠CBD=30°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
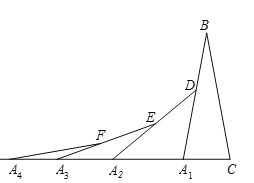
【题目】如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,按此做法继续下去,第2019个等腰三角形的底角度数是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:大家知道![]() 是无理数是无限不循环小数,因此
是无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分。又例如:因为
的整数部分是1,将这个数减去其整数部分,差就是小数部分。又例如:因为![]() ,即
,即![]() ,所以
,所以![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ,请解答下列问题:
,请解答下列问题:
(1) 如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求
的整数部分为b,求![]() 的值;
的值;
(2)已知![]() ,其中x是整数,且
,其中x是整数,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com