
【题目】综合与探究:
如图在等边三角形ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边三角形CDE,连接BE.

(1)填空:∠CAM= ;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,
①当点D在线段AM上时,求∠AOB的度数;
②当动点D在直线AM上时,试判断∠AOB是否为定值?并说明理由.
【答案】(1)30°;(2)详见解析;(3)①60°;②∠AOB是定值,∠AOB=60°,理由详见解析.
【解析】
(1)根据等边三角形的性质可以直接得出结论;
(2)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
(3)①由(2)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,由等边三角形的性质得出AM⊥BC,即可得出答案;
②分情况讨论,当点D在线段AM上时,由①得:∠AOB=60°;
当点D在线段AM的延长线上时,证明△ACD≌△BCE(SAS),得出∠CBE=∠CAD=30°即可得出答案;
当点D在线段MA的延长线上时,证明△ACD≌△BCE(SAS),得出∠CBE=∠CAD,同理得出∠CAM=30°,求出∠CBE=∠CAD=150°,得出∠CBO=30°,即可得出答案.
(1)∵△ABC是等边三角形,
∴∠BAC=60°,
∵线段AM为BC边上的中线,
∴∠CAM=![]() ∠BAC,
∠BAC,
∴∠CAM=30°,
故答案为:30°;
(2)证明:∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE,
在△ADC和△BEC中, ,
,
∴△ACD≌△BCE(SAS);
(3)①当点D在线段AM上时,如图1所示:
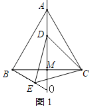
由(2)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,
∵△ABC是等边三角形,线段AM为BC边上的中线
∴AM⊥BC,
∴∠BMO=90°,
∴∠AOB=90°﹣∠CBE=90°﹣30°=60°;
②∠AOB是定值,∠AOB=60°,理由如下:
当点D在线段AM上时,由①得:∠AOB=60°;
当点D在线段AM的延长线上时,如图2所示:

∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠DCB=∠DCB+∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD=30°,
∴∠AOB=90°﹣∠CBE=90°﹣30°=60°;
当点D在线段MA的延长线上时,如图3所示:

∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠ACE=∠BCE+∠ACE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠CAD,
同理可得:∠CAM=30°
∴∠CBE=∠CAD=150°
∴∠CBO=30°,
∴∠AOB=90°﹣∠CBO=90°﹣30°=60°;
综上所述,当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点分别为A(2,4),B(﹣2,2),C(3,1).
(1)作出△ABC关于x轴对称的图形△DEF,写出顶点D、E、F的坐标.
(2)如果点H(3m﹣1,n﹣6)与点H′(2n+7,3m﹣9)关于y轴对称,求m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90天的销售单价p(元/kg)与时间t(天)之间的相关信息如图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如表,设第t天销售利润为w(元)
时间t(天) | 10 | 30 |
每天的销售量 y(kg) | 180 | 140 |
(1)分别求出售单价p(元/kg)、销售量y(kg)与时间t(天)之间的函数关系式;
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
刹车时车速/km·h-1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象.估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:Rt△ABE≌Rt△CBF
(2)若∠AEC=105°,求∠BCF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com