
����Ŀ����ʻ�е���������ɲ�������ڹ��Ե����ã���Ҫ��ǰ������һ�ξ������ֹͣ����ξ����Ϊ��ɲ����������Ϊ�˲ⶨij���ͺŵ�������ɲ������(���ٲ�����140 km/h)���������������в��ԣ�����������±���
ɲ��ʱ����/km��h��1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
ɲ������/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)�Գ���Ϊx�ᣬ��ɲ������Ϊy�ᣬ����ƽ��ֱ������ϵ�������ϱ���Ӧֵ���������Ĵ���ͼ����
(2)�۲�ͼ���ƺ��������ͣ���ȷ��һ��������Щ���ݵĺ�������ʽ��
(3)���ͺ������ڹ���������һ�ν�ͨ�¹ʣ��ֳ����ɲ������Ϊ46.5 m���Ʋ�ɲ��ʱ�ij����Ƕ��٣������¹ʷ���ʱ�������dz�����ʻ����������ʻ��
 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
��ͼ�ڵȱ�������ABC�У��߶�AMΪBC���ϵ����ߣ�����D��ֱ��AM��ʱ����CDΪһ����CD���·����ȱ�������CDE������BE��

��1����գ���CAM���� ����
��2������D���߶�AM��ʱ����֤����ADC�ա�BEC��
��3��������D��ֱ��AM��ʱ����ֱ��BE��ֱ��AM�Ľ���ΪO��
������D���߶�AM��ʱ�����AOB�Ķ�����
��������D��ֱ��AM��ʱ�����жϡ�AOB�Ƿ�Ϊ��ֵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�1����A1BC�У���B��20����A1B��CB���ڱ�A1B����ȡһ��D���ӳ�CA1��A2��ʹA1A2��A1D���õ���2����A1A2D���ڱ�A2D����ȡһ��E���ӳ�A1A2��A3��ʹA2A3��A2E���õ���3����A2A3E����������������ȥ����2019�����������εĵǶ�����______________��
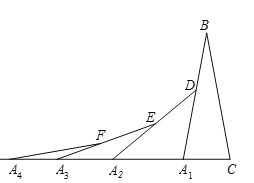
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC �ǵȱ������Σ��� P �ڡ�ABC �ڣ�PA=2������PAB �Ƶ� A ��ʱ����ת�õ���P1AC���� P1P �ij����ڣ� ��

A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ױ�BC�ij�Ϊ4�����Ϊ12����AB�Ĵ�ֱƽ����EF��AB�ڵ�E����AC�ڵ�F.��DΪBC�ߵ��е㣬MΪ�߶�EF��һ�����㣬����BDM���ܳ�����СֵΪ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��c��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����OB=OC=3������ΪM��
��1������κ����Ľ���ʽ��
��2����PΪ�߶�BM�ϵ�һ�����㣬����P��x��Ĵ���PQ������ΪQ����OQ=m���ı���ACPQ�����ΪS����S����m�ĺ�������ʽ����д��m��ȡֵ��Χ��
��3��̽�����߶�BM���Ƿ���ڵ�N��ʹ��NMCΪ���������Σ�������ڣ������N�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ļ��յ����۹���Ӧ��ij�յ����ӵ�һ�ݽ���������Ҫ����10���ڣ���10�죩�������Ϊ�������Ч�ʣ������Ӱ�ӵ㣬�ӵ�����ĵ�һ��������˿յ�42̨���Ժ�ÿ�������Ŀյ�����ǰһ���2̨�����ڻ�����ĵ�ԭ���������Ŀյ������ﵽ50̨��ÿ������һ̨���������������пյ���ƽ��ÿ̨�ɱ�������20Ԫ.
��1�����![]() �������յ�
�������յ�![]() ̨��ֱ��д��
̨��ֱ��д��![]() ��
��![]() ֮��ĺ�������ʽ����д���Ա���
֮��ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2����ÿ̨�յ��ijɱ��ۣ���������������50̨ʱ��Ϊ2000Ԫ�������۸�Ϊÿ̨2920Ԫ�����![]() �������Ϊ
�������Ϊ![]() Ԫ������
Ԫ������![]() ��
��![]() ֮��ĺ�������ʽ��������һ���õ����������������Ƕ���.
֮��ĺ�������ʽ��������һ���õ����������������Ƕ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У���BAC=90����AB=AC.MN�ǹ���A��ֱ�ߣ�BD��MN ��D��CE��MN��E.
��1����֤��BD=AE.
��2������MN�Ƶ�A��ת��ʹMN��BC�ཻ�ڵ�G(��ͼ2)�������������䣬��֤��BD=AE.
��3����(2)������£���CE���ӳ��߹�AB���е�F����ͼ3��������GF����֤����AFE=��BFG.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com