
ЁОЬтФПЁПдФЖСРэНтЃКЖдгкx3ЉЃЈn2+1ЃЉx+nетРрЬиЪтЕФДњЪ§ЪНПЩвдАДЯТУцЕФЗНЗЈЗжНтвђЪНЃК
x3ЉЃЈn2+1ЃЉx+nЃНx3Љn2xЉx+nЃНxЃЈx2Љn2ЃЉЉЃЈxЉnЃЉЃНxЃЈxЉnЃЉЃЈx+nЃЉЉЃЈxЉnЃЉЃНЃЈxЉnЃЉЃЈx2+nxЉ1ЃЉЃЎ
РэНтдЫгУЃКШчЙћx3ЉЃЈn2+1ЃЉx+nЃН0ЃЌФЧУДЃЈxЉnЃЉЃЈx2+nxЉ1ЃЉЃН0ЃЌМДгаxЉnЃН0Лђx2+nxЉ1ЃН0ЃЌ
вђДЫЃЌЗНГЬxЉnЃН0КЭx2+nxЉ1ЃН0ЕФЫљгаНтОЭЪЧЗНГЬx3ЉЃЈn2+1ЃЉx+nЃН0ЕФНтЃЎ
НтОіЮЪЬтЃКЧѓЗНГЬx3Љ5x+2ЃН0ЕФНтЮЊ_____ЃЎ
ЁОД№АИЁПxЃН2ЛђxЃНЉ1+![]() ЛђxЃНЉ1Љ
ЛђxЃНЉ1Љ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
НЋдЗНГЬзѓБпБфаЮЮЊx3Љ4xЉx+2ЃН0ЃЌдйНјвЛВНвђЪНЗжНтЕУЃЈxЉ2ЃЉ[xЃЈx+2ЃЉЉ1]ЃН0ЃЌОнДЫЕУЕНСНИіЙигкxЕФЗНГЬЧѓНтПЩЕУЃЎ
НтЃКЁпx3Љ5x+2ЃН0ЃЌ
Ёрx3Љ4xЉx+2ЃН0ЃЌ
ЁрxЃЈx2Љ4ЃЉЉЃЈxЉ2ЃЉЃН0ЃЌ
ЁрxЃЈx+2ЃЉЃЈxЉ2ЃЉЉЃЈxЉ2ЃЉЃН0ЃЌ
дђЃЈxЉ2ЃЉ[xЃЈx+2ЃЉЉ1]ЃН0ЃЌМДЃЈxЉ2ЃЉЃЈx2+2xЉ1ЃЉЃН0ЃЌ
ЁрxЉ2ЃН0Лђx2+2xЉ1ЃН0ЃЌ
НтЕУxЃН2ЛђxЃНЉ1![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃКxЃН2ЛђxЃНЉ1+![]() ЛђxЃНЉ1Љ
ЛђxЃНЉ1Љ![]() ЃЎ
ЃЎ


 ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсЕФНЛЕузјБъЮЊ
жсЕФНЛЕузјБъЮЊ![]() КЭ
КЭ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() ЃЈгУ
ЃЈгУ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉШєдкздБфСП![]() ЕФжЕТњзу
ЕФжЕТњзу![]() ЕФЧщПіЯТЃЌгыЦфЖдгІЕФКЏЪ§жЕ
ЕФЧщПіЯТЃЌгыЦфЖдгІЕФКЏЪ§жЕ![]() ЕФзюДѓжЕЮЊ1ЃЌЧѓ
ЕФзюДѓжЕЮЊ1ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉвбжЊЕу![]() КЭЕу
КЭЕу![]() ЃЎШєЖўДЮКЏЪ§
ЃЎШєЖўДЮКЏЪ§![]() ЕФЭМЯѓгыЯпЖЮ
ЕФЭМЯѓгыЯпЖЮ![]() гаСНИіВЛЭЌЕФНЛЕуЃЌжБНгаДГі
гаСНИіВЛЭЌЕФНЛЕуЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌвбжЊЕу![]() дке§ЗНаЮ
дке§ЗНаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ДЙзуЮЊЕу
ДЙзуЮЊЕу![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЎ
ЃЎ
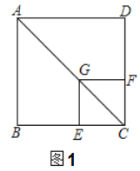
ЃЈ1ЃЉжЄУїгыЭЦЖЯЃК
![]() ЧѓжЄЃКЫФБпаЮ
ЧѓжЄЃКЫФБпаЮ![]() ЪЧе§ЗНаЮЃЛ
ЪЧе§ЗНаЮЃЛ
![]() ЭЦЖЯЃК
ЭЦЖЯЃК![]() ЕФжЕЮЊ_ _ЃЛ
ЕФжЕЮЊ_ _ЃЛ
ЃЈ2ЃЉЬНОПгыжЄУїЃК
НЋе§ЗНаЮ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыЗНЯђа§зЊ
ЫГЪБеыЗНЯђа§зЊ![]() НЧ
НЧ![]() ЃЌШчЭМЃЈ2ЃЉЫљЪОЃЌЪдЬНОПЯпЖЮ
ЃЌШчЭМЃЈ2ЃЉЫљЪОЃЌЪдЬНОПЯпЖЮ![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙгыдЫгУЃК
Шє![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() дкШЦЕу
дкШЦЕу![]() а§зЊЙ§ГЬжаЃЌЕБ
а§зЊЙ§ГЬжаЃЌЕБ![]() Ш§ЕудквЛЬѕжБЯпЩЯЪБЃЌдђ
Ш§ЕудквЛЬѕжБЯпЩЯЪБЃЌдђ![]() ЃЎ
ЃЎ
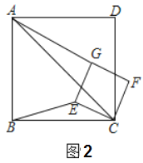
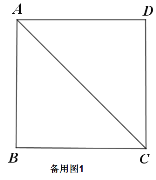
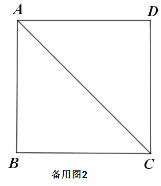
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЃЌ
ЃЌ![]() ЩЯЕФЕуЃЌЧв
ЩЯЕФЕуЃЌЧв![]() ЃЎ
ЃЎ
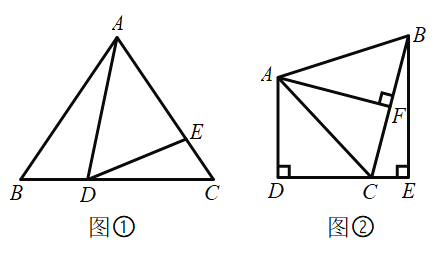
ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() дк
дк![]() жсЩЯЃЌ
жсЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЗДБШР§КЏЪ§
ЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЎ
ЃЎ
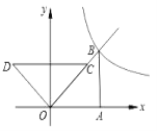
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉАб![]() биЩфЯп
биЩфЯп![]() вЦЖЏЃЌЕБЕу
вЦЖЏЃЌЕБЕу![]() Тфдк
Тфдк![]() ЭМЯѓЩЯЕФ
ЭМЯѓЩЯЕФ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
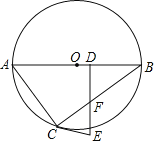
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌCЪЧЁбOЩЯЕФвЛЕуЃЌDЪЧABЩЯЕФвЛЕуЃЌDEЁЭABгкDЃЌDEНЛBCгкFЃЌЧвEFЃНECЃЎ
ЃЈ1ЃЉЧѓжЄЃКECЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєBDЃН4ЃЌBCЃН8ЃЌдВЕФАыОЖOBЃН5ЃЌЧѓЧаЯпECЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
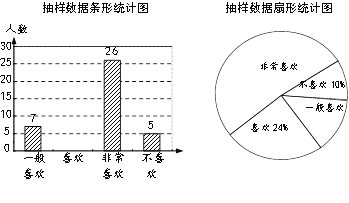
ЁОЬтФПЁПФГаЃгУЫцЛњГщбљЕФЗНЗЈдкОХФъМЖПЊеЙСЫЁАФуЪЧЗёЯВЛЖЭјПЮЁБЕФЕїВщЃЌВЂНЋЕУЕНЕФЪ§ОнећРэГЩСЫвдЯТЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
ЃЈ1ЃЉДЫДЮЙВЕїВщСЫ УћбЇЩњЃЛ
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєИУбЇаЃОХФъМЖЙВга300УћбЇЩњЃЌЧыФуЙРМЦЦфжаЁАЗЧГЃЯВЛЖЁБЭјПЮЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЮвЪаЁАЧрЩНТЬЫЎЁБааЖЏжаЃЌФГЩчЧјМЦЛЎЖдУцЛ§ЮЊ![]() ЕФЧјгђНјааТЬЛЏЃЌОЭЖБъгЩМзЁЂввСНИіЙЄГЬЖгРДЭъГЩЃЎвбжЊМзЖгУПЬьФмЭъГЩТЬЛЏЕФУцЛ§ЪЧввЖгУПЬьФмЭъГЩТЬЛЏУцЛ§ЕФ2БЖЃЌШчЙћСНЖгИїздЖРСЂЭъГЩУцЛ§ЮЊ
ЕФЧјгђНјааТЬЛЏЃЌОЭЖБъгЩМзЁЂввСНИіЙЄГЬЖгРДЭъГЩЃЎвбжЊМзЖгУПЬьФмЭъГЩТЬЛЏЕФУцЛ§ЪЧввЖгУПЬьФмЭъГЩТЬЛЏУцЛ§ЕФ2БЖЃЌШчЙћСНЖгИїздЖРСЂЭъГЩУцЛ§ЮЊ![]() ЧјгђЕФТЬЛЏЪБЃЌМзЖгБШввЖгЩйгУ6ЬьЃЎ
ЧјгђЕФТЬЛЏЪБЃЌМзЖгБШввЖгЩйгУ6ЬьЃЎ
(1)ЧѓМзЁЂввСНЙЄГЬЖгУПЬьИїФмЭъГЩЖрЩйУцЛ§ЕФТЬЛЏЃЛ
(2)ШєМзЖгУПЬьТЬЛЏЗбгУЪЧ1.2ЭђдЊЃЌввЖгУПЬьТЬЛЏЗбгУЮЊ0.5ЭђдЊЃЌЩчЧјвЊЪЙетДЮТЬЛЏЕФзмЗбгУВЛГЌЙ§40ЭђдЊЃЌдђжСЩйгІАВХХввЙЄГЬЖгТЬЛЏЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭјТчЯњЪлЪЧвЛжжживЊЕФЯњЪлЗНЪНЃЎФГЯчеђХЉУГЙЋЫОаТПЊЩшСЫвЛМвЭјЕъЃЌЯњЪлЕБЕиХЉВњЦЗЃЎЦфжавЛжжЕБЕиЬиВњдкЭјЩЯЪдЯњЪлЃЌЦфГЩБОЮЊУПЧЇПЫ10дЊЃЎЙЋЫОдкЪдЯњЪлЦкМфЃЌЕїВщЗЂЯжЃЌУПЬьЯњЪлСПyЃЈkgЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉТњзуШчЭМЫљЪОЕФКЏЪ§ЙиЯЕЃЈЦфжа![]() ЃЉЃЎ
ЃЉЃЎ
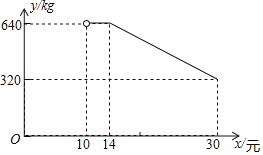
ЃЈ1ЃЉжБНгаДГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНМАздБфСПЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉШєХЉУГЙЋЫОУПЬьЯњЪлИУЬиВњЕФРћШѓвЊДяЕН3100дЊЃЌдђЯњЪлЕЅМлxгІЖЈЮЊЖрЩйдЊЃП
ЃЈ3ЃЉЩшУПЬьЯњЪлИУЬиВњЕФРћШѓЮЊWдЊЃЌШє![]() ЃЌЧѓЃКЯњЪлЕЅМлxЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЌЧѓЃКЯњЪлЕЅМлxЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com