
ЁОЬтФПЁПФГвНвЉбаОПЫљбаЗЂСЫвЛжжаТвЉЃЌЪдбщвЉаЇЪБЗЂЯжЃК1.5аЁЪБФкЃЌбЊвКжаКЌвЉСПyЃЈЮЂПЫЃЉгыЪБМфxЃЈаЁЪБЃЉЕФЙиЯЕПЩНќЫЦЕигУЖўДЮКЏЪ§yЃНax2+bxБэЪОЃЛ1.5аЁЪБКѓЃЈАќРЈ1.5аЁЪБЃЉЃЌyгыxПЩНќЫЦЕигУЗДБШР§КЏЪ§yЃН![]() ЃЈkЃО0ЃЉБэЪОЃЌВПЗжЪЕбщЪ§ОнШчБэЃК
ЃЈkЃО0ЃЉБэЪОЃЌВПЗжЪЕбщЪ§ОнШчБэЃК
ЪБМфxЃЈаЁЪБЃЉ | 0.2 | 1 | 1.8 | Ё |
КЌвЉСПyЃЈЮЂПЫЃЉ | 7.2 | 20 | 12.5 | Ё |
ЃЈ1ЃЉЧѓaЁЂbМАkЕФжЕЃЛ
ЃЈ2ЃЉЗўвЉКѓМИаЁЪБбЊвКжаЕФКЌвЉСПДяЕНзюДѓжЕЃПзюДѓжЕЮЊЖрЩйЃП
ЃЈ3ЃЉШчЙћУПКСЩ§бЊвКжаКЌвЉСПВЛЩйгк10ЮЂПЫЪБжЮСЦМВВЁгааЇЃЌФЧУДГЩШЫАДЙцЖЈМССПЗўгУИУвЉвЛДЮКѓФмЮЌГжЖрГЄЕФгааЇЪБМфЃЎЃЈ![]() Ёж1.41ЃЌОЋШЗЕН0.1аЁЪБЃЉ
Ёж1.41ЃЌОЋШЗЕН0.1аЁЪБЃЉ
ЁОД№АИЁПЃЈ1ЃЉaЃНЉ20ЃЌbЃН40ЃЌkЃН22.5ЃЛЃЈ2ЃЉЗўвЉКѓ1аЁЪБбЊвКжаЕФКЌвЉСПДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ20ЮЂПЫЃЛЃЈ3ЃЉГЩШЫАДЙцЖЈМССПЗўгУИУвЉвЛДЮКѓФмЮЌГж2.0аЁЪБЕФгааЇЪБМфЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнБэИёаХЯЂДњШыЪ§жЕСаЗНГЬзщЧѓНтМДПЩЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕУЕНyЃНЉ20x2+40xЃЌЛЏЮЊЖЅЕуЪНМДПЩЕУЕННсЙћЃЛ
ЃЈ3ЃЉСюy=10ЧѓГіxЕФжЕОЭЪЧЫљЧѓЕФНсЙћЃЛ
ЃЈ1ЃЉЩш1.5аЁЪБФкЃЌбЊвКжаКЌвЉСПyЃЈЮЂПЫЃЉгыЪБМфxЃЈаЁЪБЃЉЕФЙиЯЕЮЊyЃНax2+bxЃЌ
ИљОнБэИёЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃКaЃНЉ20ЃЌbЃН40ЃЌ
1.5аЁЪБКѓЃЈАќРЈ1.5аЁЪБЃЉЃЌyгыxПЩНќЫЦЕигУЗДБШР§КЏЪ§yЃН![]() ЃЈkЃО0ЃЉЃЌИљОнБэИёЕУЃК
ЃЈkЃО0ЃЉЃЌИљОнБэИёЕУЃК
kЃН1.8ЁС12.5ЃН22.5ЃЌ
ЁрaЃНЉ20ЃЌbЃН40ЃЌkЃН22.5ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊyЃНЉ20x2+40xЃЌ
ЁрyЃНЉ20ЃЈxЉ1ЃЉ2+20ЃЌ
ЁрЗўвЉКѓ1аЁЪБбЊвКжаЕФКЌвЉСПДяЕНзюДѓжЕЃЌзюДѓжЕЮЊ20ЮЂПЫЃЛ
ЃЈ3ЃЉЕБyЃН10ЪБЃЌ10ЃНЉ20x2+40xЃЌЛђ10ЃН![]() ЃЌ
ЃЌ
НтЕУЃКxЃН1Љ![]() ЛђxЃН1+
ЛђxЃН1+![]() ЃЈxЃО1.5ЃЌВЛКЯЬтвтЩсШЅЃЉЃЌxЃН2.25ЃЌ
ЃЈxЃО1.5ЃЌВЛКЯЬтвтЩсШЅЃЉЃЌxЃН2.25ЃЌ
ЁрГЩШЫАДЙцЖЈМССПЗўгУИУвЉвЛДЮКѓФмЮЌГж2.25ЉЃЈ1Љ![]() ЃЉЁж2.0аЁЪБЕФгааЇЪБМфЃЎ
ЃЉЁж2.0аЁЪБЕФгааЇЪБМфЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
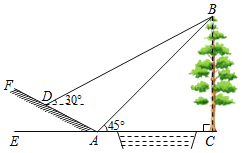
ЁОЬтФПЁПШчЭМЃЌаЁУїЮЊСЫВтСПаЁКгЖдАЖДѓЪїBCЕФИпЖШЃЌЫћдкЕуAВтЕУДѓЪїЖЅЖЫBЕФбіНЧЮЊ45ЁуЃЌбиаБЦТзп3![]() УзЕНДяаБЦТЩЯЕуDЃЌдкДЫДІВтЕУЪїЖЅЖЫЕуBЕФбіНЧЮЊ30ЁуЃЌЧваБЦТAFЕФЦТБШЮЊ1ЃК2ЃЎЧѓДѓЪїBCЕФИпЖШдМЮЊЖрЩйУзЃПЃЈ
УзЕНДяаБЦТЩЯЕуDЃЌдкДЫДІВтЕУЪїЖЅЖЫЕуBЕФбіНЧЮЊ30ЁуЃЌЧваБЦТAFЕФЦТБШЮЊ1ЃК2ЃЎЧѓДѓЪїBCЕФИпЖШдМЮЊЖрЩйУзЃПЃЈ![]() Ёж1.732ЃЌНсЙћОЋШЗЕН0.1ЃЉ
Ёж1.732ЃЌНсЙћОЋШЗЕН0.1ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЩЬиЪтЕНвЛАуЁЂРрБШЁЂзЊЛЏЪЧЪ§бЇбЇЯАКЭбаОПжаОГЃгУЕНЕФЫМЯыЗНЗЈЃЌЯТУцЪЧЖдвЛЕРМИКЮЬтНјааБфЪНЬНОПЕФЫМТЗЃЌЧыФудЫгУЩЯЪіЫМЯыЗНЗЈЭъГЩЬНОПШЮЮёЃЎ
ЮЪЬтЧщОГЃКдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧЖдНЧЯпЃЌ
ЪЧЖдНЧЯпЃЌ![]() ЮЊБп
ЮЊБп![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() .вд
.вд![]() ЮЊа§зЊжааФЃЌНЋЯпЖЮ
ЮЊа§зЊжааФЃЌНЋЯпЖЮ![]() ЫГЪБеыа§зЊЃЌа§зЊНЧгы
ЫГЪБеыа§зЊЃЌа§зЊНЧгы![]() ЯрЕШЃЌЕУЕНЯпЖЮ
ЯрЕШЃЌЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЬиР§ШчЭМ1ЃЌШєЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌдђ
ЪЧе§ЗНаЮЃЌдђ![]() гы
гы![]() ЮЛжУЙиЯЕЪЧ_________ЃЎДЫЪБПЩвдЙ§Еу
ЮЛжУЙиЯЕЪЧ_________ЃЎДЫЪБПЩвдЙ§Еу![]() зї
зї![]() ЕФЦНааЯпРДЖдНсТлНјаажЄУїЃЈетРяВЛвЊЧѓжЄУїЃЉ
ЕФЦНааЯпРДЖдНсТлНјаажЄУїЃЈетРяВЛвЊЧѓжЄУїЃЉ
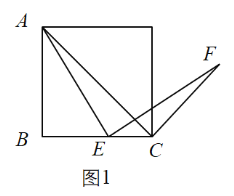
ЃЈ2ЃЉЭиеЙЬНОПЃКШчЭМ2ЃЌШєЫФБпаЮ![]() ЪЧСтаЮЃЌЕБ
ЪЧСтаЮЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() гыxжсЁЂyжсЗжБ№ЯрНЛгкAЃЌBСНЕуЃЌгыЗДБШР§КЏЪ§
гыxжсЁЂyжсЗжБ№ЯрНЛгкAЃЌBСНЕуЃЌгыЗДБШР§КЏЪ§![]() дкЕкЖўЯѓЯоФкНЛгкЕуCЃЌЧвЕуBЪЧ
дкЕкЖўЯѓЯоФкНЛгкЕуCЃЌЧвЕуBЪЧ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
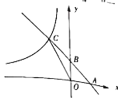
ЃЈ1ЃЉЧѓЕуCЕФзјБъМАkЕФжЕЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіОиаЮЕФУцЛ§ЮЊ96000000cm2ЃЌЕквЛДЮНиШЅЫќЕФ![]() ЃЌЕкЖўДЮНиШЅЪЃЯТЕФ
ЃЌЕкЖўДЮНиШЅЪЃЯТЕФ![]() ЃЌШчДЫНиЯТШЅЃЌЕкСљДЮНиШЅКѓЪЃгрЭМаЮЕФУцЛ§ЮЊ_____cm2ЃЌгУПЦбЇМЧЪ§ЗЈБэЪОЪЃгрЭМаЮЕФУцЛ§ЮЊ_____cm2ЃЎ
ЃЌШчДЫНиЯТШЅЃЌЕкСљДЮНиШЅКѓЪЃгрЭМаЮЕФУцЛ§ЮЊ_____cm2ЃЌгУПЦбЇМЧЪ§ЗЈБэЪОЪЃгрЭМаЮЕФУцЛ§ЮЊ_____cm2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
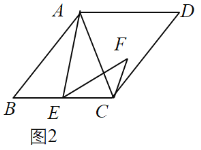
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЮЊЁбOЩЯвЛЕуЃЌОЙ§ЕуCЕФЧаЯпНЛABЕФбгГЄЯпгкЕуEЃЌADЁЭECНЛECЕФбгГЄЯпгкЕуDЃЌADНЛЁбOгкFЃЌFMЁЭABгкHЃЌЗжБ№НЛЁбOЁЂACгкMЁЂNЃЌСЌНгMBЃЌBCЃЎ
ЃЈ1ЃЉЧѓжЄЃКACЦНЗжЁЯDAEЃЛ
ЃЈ2ЃЉШєcosM=![]() ЃЌBE=1ЃЌЂйЧѓЁбOЕФАыОЖЃЛЂкЧѓFNЕФГЄЃЎ
ЃЌBE=1ЃЌЂйЧѓЁбOЕФАыОЖЃЛЂкЧѓFNЕФГЄЃЎ
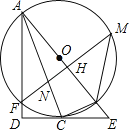
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЕуDдкACЩЯЃЌЧвCD>DAЃЌDA=2ЃЎЕуPЁЂQЭЌЪБДгDЕуГіЗЂЃЌвдЯрЭЌЕФЫйЖШЗжБ№биЩфЯпDCЁЂЩфЯпDAдЫЖЏЃЎЙ§ЕуQзїACЕФДЙЯпЖЮQRЃЌЪЙQR=PQЃЌСЊНгPRЃЎЕБЕуQЕНДяAЪБЃЌЕуPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЎЩшPQ=xЃЎЁїPQRКЭЁїABCжиКЯВПЗжЕФУцЛ§ЮЊSЃЎSЙигкxЕФКЏЪ§ЭМЯёШчЭМ2ЫљЪОЃЈЦфжа0<xЁм![]() ЃЌ
ЃЌ![]() <xЁмmЪБЃЌКЏЪ§ЕФНтЮіЪНВЛЭЌЃЉ
<xЁмmЪБЃЌКЏЪ§ЕФНтЮіЪНВЛЭЌЃЉ
ЃЈ1ЃЉЬюПеЃКnЕФжЕЮЊ___________;
ЃЈ2ЃЉЧѓSЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЎ
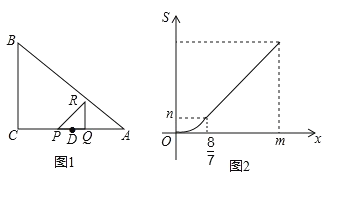
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНmx+nЃЈmЁй0ЃЉЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФЕуA(aЃЌ4)КЭЕуB(8ЃЌЉ1)ЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФЕуA(aЃЌ4)КЭЕуB(8ЃЌЉ1)ЃЎ
ЃЈ1ЃЉЗжБ№ЧѓГівЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉбгГЄAOгыЗДБШР§КЏЪ§НЛгкЕуCЃЌСЌНгBCЃЌЧѓ![]() ABCЕФУцЛ§ЃЎ
ABCЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСвдЯТВФСЯЃКЖдЪ§ЕФДДЪМШЫЪЧЫеИёРМЪ§бЇМвФЩЦЄЖћЃЈJЃЎNapierЃЌ1550Фъ-1617ФъЃЉЃЌФЩЦЄЖћЗЂУїЖдЪ§ЪЧдкжИЪ§ИХФюНЈСЂжЎЧАЃЌжБЕН18ЪРМЭШ№ЪПЪ§бЇМвХЗРЃЈEulerЃЌ1707Фъ-1783ФъЃЉВХЗЂЯжжИЪ§гыЖдЪ§жЎМфЕФСЊЯЕЃЎЖдЪ§ЕФЖЈвхЃКвЛАуЕиЃЌШє![]() ЃЌдђ
ЃЌдђ![]() Назівд
Назівд![]() ЮЊЕз
ЮЊЕз![]() ЕФЖдЪ§ЃЌМЧзї
ЕФЖдЪ§ЃЌМЧзї![]() ЃЎБШШчжИЪ§ЪН
ЃЎБШШчжИЪ§ЪН![]() ПЩвдзЊЛЏЮЊ
ПЩвдзЊЛЏЮЊ![]() ЃЌЖдЪ§ЪН
ЃЌЖдЪ§ЪН![]() ПЩвдзЊЛЏЮЊ
ПЩвдзЊЛЏЮЊ![]() ЃЎЮвУЧИљОнЖдЪ§ЕФЖЈвхПЩЕУЕНЖдЪ§ЕФвЛИіаджЪЃК
ЃЎЮвУЧИљОнЖдЪ§ЕФЖЈвхПЩЕУЕНЖдЪ§ЕФвЛИіаджЪЃК![]()
![]() ЃЎРэгЩШчЯТЃКЩш
ЃЎРэгЩШчЯТЃКЩш![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌгЩЖдЪ§ЕФЖЈвхЕУ
ЃЌгЩЖдЪ§ЕФЖЈвхЕУ![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЎНтОівдЯТЮЪЬтЃК
ЃЎНтОівдЯТЮЪЬтЃК
ЃЈ1ЃЉНЋжИЪ§![]() зЊЛЏЮЊЖдЪ§ЪНЃК ЃЎ
зЊЛЏЮЊЖдЪ§ЪНЃК ЃЎ
ЃЈ2ЃЉЗТееЩЯУцЕФВФСЯЃЌЪджЄУїЃК![]()
ЃЈ3ЃЉЭиеЙдЫгУЃКМЦЫу![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com