
【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=![]() ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.
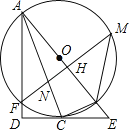
【答案】(1)证明见解析;(2)①⊙O的半径为4;②FN=![]() .
.
【解析】(1)连接OC,如图,利用切线的性质得OC⊥DE,则判断OC∥AD得到∠1=∠3,加上∠2=∠3,从而得到∠1=∠2;
(2)①利用圆周角定理和垂径定理得到![]() ,则∠COE=∠FAB,所以∠FAB=∠M=∠COE,设⊙O的半径为r,然后在Rt△OCE中利用余弦的定义得到
,则∠COE=∠FAB,所以∠FAB=∠M=∠COE,设⊙O的半径为r,然后在Rt△OCE中利用余弦的定义得到![]() ,从而解方程求出r即可;
,从而解方程求出r即可;
②连接BF,如图,先在Rt△AFB中利用余弦定义计算出AF=![]() ,再计算出OC=3,接着证明△AFN∽△AEC,然后利用相似比可计算出FN的长.
,再计算出OC=3,接着证明△AFN∽△AEC,然后利用相似比可计算出FN的长.
(1)连接OC,如图,
∵直线DE与⊙O相切于点C,
∴OC⊥DE,
又∵AD⊥DE,
∴OC∥AD.
∴∠1=∠3
∵OA=OC,
∴∠2=∠3,
∴∠1=∠2,
∴AC平方∠DAE;
(2)①∵AB为直径,
∴∠AFB=90°,
而DE⊥AD,
∴BF∥DE,
∴OC⊥BF,
∴![]() ,
,
∴∠COE=∠FAB,
而∠FAB=∠M,
∴∠COE=∠M,
设⊙O的半径为r,
在Rt△OCE中,cos∠COE=![]() ,即
,即![]() ,解得r=4,
,解得r=4,
即⊙O的半径为4;
②连接BF,如图,
在Rt△AFB中,cos∠FAB=![]() ,
,
∴AF=8×![]() ,
,
在Rt△OCE中,OE=5,OC=4,
∴CE=3,
∵AB⊥FM,
∴![]() ,
,
∴∠5=∠4,
∵FB∥DE,
∴∠5=∠E=∠4,
∵![]() ,
,
∴∠1=∠2,
∴△AFN∽△AEC,
∴![]() ,即
,即![]() ,
,
∴FN=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)[(-3a2b3)3]2;
(2)(-2xy2)6+(-3x2y4)3;
(3)![]() ;
;
(4)(0.5×3![]() )199×(-2×
)199×(-2×![]() )200.
)200.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题;
(1)4(a3)4﹣(3a6)2
(2)﹣6xy(x﹣2y)
(3)(9x2y﹣6xy2)÷3xy
(4)(a+2b)(a﹣2b)﹣(a+b)2
(5)(﹣12)0+2﹣2
(6)20182﹣2017×2019(用公式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到等式(a+b)2=a2+2ab+b2,请解各下列问题:
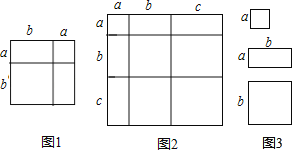
(1)写出图2中所表示的数学等式 .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x= ,y= ,z= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
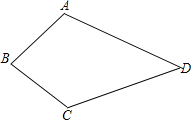
【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在规格为8×8的边长为1个单位的正方形网格中(每个小正方形的边长为1),![]() 的三个顶点都在格点上,且直线
的三个顶点都在格点上,且直线![]() 、
、![]() 互相垂直.
互相垂直.
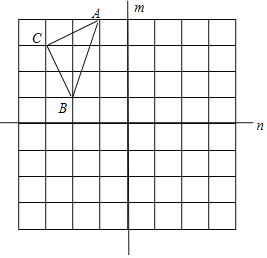
(1)画出![]() 关于直线
关于直线![]() 的轴对称图形
的轴对称图形![]() ;
;
(2)在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的周长最小(保留画图痕迹);周长的最小值为_____;
的周长最小(保留画图痕迹);周长的最小值为_____;
(3)试求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com