
【题目】如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°
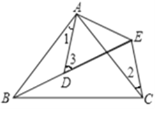
(1)求证△ABD≌△ACE
(2)求∠3度数.
科目:初中数学 来源: 题型:
【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
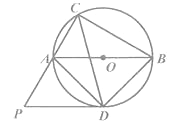
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过原点O(0,0),点A(1,1),点B(![]() ,0).
,0).
(1)求抛物线解析式;
(2)连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积;
(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似,若存在,求出点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
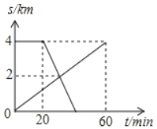
A. 8:30 B. 8:35 C. 8:40 D. 8:45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十一黄金周某一天,甲、乙两名学生去距家36千米的风景区游玩,他们从家出发,骑电动车行驶20分钟时发现忘带相机,甲下车步行前往,乙骑电动车按原路返回,乙取到相机后(在家取相机所用时间忽略不计),骑电动车追甲,在距风景区13.5千米处追上甲并同车前往风景区,若电动车速度始终不变.设甲与家相距![]() (千米),乙与家相距
(千米),乙与家相距![]() (千米),甲离开家的时间为
(千米),甲离开家的时间为![]() (分钟),
(分钟),![]() 、
、![]() 与x之间的函数图象如图所示,结合图象解答下列问题:
与x之间的函数图象如图所示,结合图象解答下列问题:

(1)求电动车的速度;
(2)求出甲步行的时间是多少分钟?;
(3)求乙返回到家时,甲与家相距多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
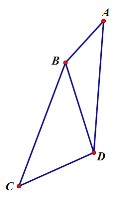
【题目】如图,BD为四边形ABCD的对角线,BC=AD,∠A=∠CBD,∠ABD=120°,AB=3,CD=![]() ,则BC的长为_____________.
,则BC的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在孝感市关工委组织的“五好小公民”主题教育活动中,我市蓝天学校组织全校学生参加了“红旗飘飘,引我成长”知识竞赛,赛后随机抽取了部分参赛学生的成绩,按从高分到低分将成绩分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五类,绘制成下面两个不完整的统计图:
五类,绘制成下面两个不完整的统计图:
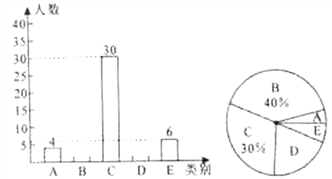
根据上面提供的信息解答下列问题:
(1)![]() 类所对应的圆心角是________度,样本中成绩的中位数落在________类中,并补全条形统计图;
类所对应的圆心角是________度,样本中成绩的中位数落在________类中,并补全条形统计图;
(2)若![]() 类含有2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图求恰好抽到1名男生和1名女生的概率.
类含有2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
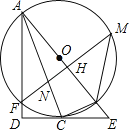
【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=![]() ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com