
【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
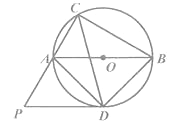
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
【答案】见解析
【解析】(1)根据角平分线的定义得出∠1=∠3,得出弧AD=弧BD,根据垂径定理可得出OD⊥AB,再根据PD∥AB,就可证得OD⊥PD,即可得证;
(2)根据圆内接四边形的定理,可证得∠2=∠CBD,再根据圆周角定理及等腰直角三角形的性质,可证得∠ADP=∠1,然后根据相似三角形的判定定理,可证得结论.
(1)证明:如图,连接OD
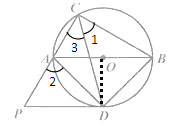
∵CD平分∠ACB
∴∠1=∠3
∴弧AD=弧BD
∴OD⊥AB
∵PD∥AB
∴OD⊥PD
∵OD是半径
∴PD是⊙O的切线
(2)证明:∵四边形ADBC是圆的内接四边形,
∴∠CAD+∠CBD=180°
∵∠2+∠CAD=180°
∴∠2=∠CBD
∵AB是圆的直径
∴∠ADO+∠BDO=90°,∠1+∠3=90°,即∠1=45°
∵弧AD=弧BD,OD⊥AB
∴AD=BD
∴∠ADO=45°
∵∠ADO+∠ADP=90°
∴∠ADP=45°=∠1
∴△PAD∽△DBC


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
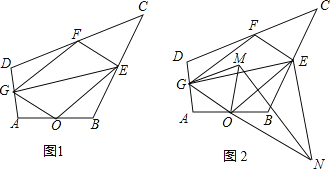
【题目】如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.
①若OE=![]() ,OG=1,求
,OG=1,求![]() 的值;
的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工分别住在![]() 三个住宅区,
三个住宅区,![]() 区有
区有![]() 人,
人,![]() 区有
区有![]() 人,
人,![]() 区有
区有![]() 人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )
人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )

A.![]() 区B.
区B.![]() 区C.
区C.![]() 区D.不确定
区D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
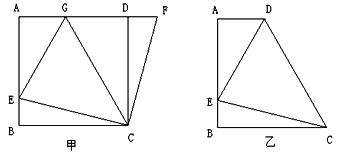
【题目】如图(甲),在正方形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() ;
;
(2)在如图(甲)中,若![]() 在
在![]() 上,且
上,且![]() ,则
,则![]() 成立吗?
成立吗?
证明你的结论.(3)运用(1)(2)解答中积累的经验和知识,完成下题:
如图(乙)四边形![]() 中,
中,![]() ∥
∥![]() (
(![]() >
>![]() ),
),![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市设计的长方形休闲广场如图所示,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池.
(1)用图中所标字母表示广场空地(图中阴影部分)的面积.
(2)若休闲广场的长为90米,宽为40米,求广场空地的面积(计算结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AD∥BC,AD=5,B(-3,0),C(9,0),点E是BC的中点,点P是线段BC上一动点,当PB=________时,以点P、A、D、E为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(6)班为从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评.其中,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表;另全班50位同学参与民主测评进行投票,结果如下图:
![]()
A | B | C | D | E | |
甲 | 89 | 91 | 92 | 94 | 93 |
乙 | 90 | 86 | 85 | 91 | 94 |

规定: 演讲得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两位选手各自演讲答辩的平均分;
(2)民主测评统计图中a= ,b= ;
(3)求甲、乙两位选手的民主测评得分;
(4)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com