
【题目】某公司员工分别住在![]() 三个住宅区,
三个住宅区,![]() 区有
区有![]() 人,
人,![]() 区有
区有![]() 人,
人,![]() 区有
区有![]() 人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )
人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )

A.![]() 区B.
区B.![]() 区C.
区C.![]() 区D.不确定
区D.不确定
科目:初中数学 来源: 题型:
【题目】阅读下面材料
在数学课上,老师提出如下问题:
己知:已知:Rt△ABC,∠ABC=90°.
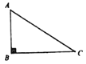
求作:矩形ABCD.
小敏的作法如下:
①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;
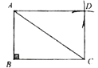
②连接DA、DC;所以四边形ABCD为所求矩形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是(-2,0)、(0,4).动点P从O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止,点C停止运动时点P也随之停止运动.以CP、CO为邻边构造□PCOD,在线段OP的延长线长取点E,使得PE=2.设点P的运动时间为t秒.

(1)求证:四边形ADEC是平行四边形;
(2)以线段PE为对角线作正方形MPNE,点M、N分别在第一、四象限.
①当点M、N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M、N中恰好只有一点落在四边形ADEC的内部(不包括边界)时,设□PCOD的面积为S,直接写出S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冰封文教店用1200元购进了甲、乙两种钢笔,已知甲种钢笔进价为每支12元,乙种钢笔进价为每支10元。在销售时甲种钢笔售价为每支15元,乙种钢笔售价为每支12元,全部售完后共获利270元。
(1)求冰封文教店购进甲、乙两种钢笔各多少支?
(2)冰封文教店以原价再次购进甲、乙两种钢笔,且购进甲种钢笔的数量不变,而购进乙种钢笔的数量是第一次的2倍,乙种钢笔按原售价销售,而甲种钢笔降价销售,当两种钢笔销售完毕时,要使再次购进的钢笔获利不少于340元,甲种钢笔每支最低售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知AB是⊙O 的直径,C是⊙O 上一点,∠ACB的平分线交⊙O 于点D,作PD∥AB,交CA的延长线于点P.连结AD,BD.
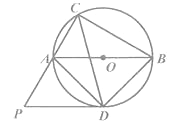
求证:(1)PD是⊙O 的切线;
(2)△PAD![]() △DBC.
△DBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com