
【题目】阅读下面材料
在数学课上,老师提出如下问题:
己知:已知:Rt△ABC,∠ABC=90°.
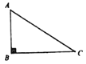
求作:矩形ABCD.
小敏的作法如下:
①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;
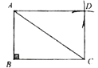
②连接DA、DC;所以四边形ABCD为所求矩形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是____________________.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴分别交于原点
轴分别交于原点![]() 和点
和点![]() ,与对称轴
,与对称轴![]() 交于点
交于点![]() .矩形
.矩形![]() 的边
的边![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,边
,边![]() ,
,![]() 与抛物线分别交于点
与抛物线分别交于点![]() ,
,![]() .当矩形
.当矩形![]() 沿
沿![]() 轴正方向平移,点
轴正方向平移,点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的同侧时,连接
的同侧时,连接![]() ,此时,四边形
,此时,四边形![]() 的面积记为
的面积记为![]() ;点
;点![]() ,
,![]() 位于对称轴
位于对称轴![]() 的两侧时,连接
的两侧时,连接![]() ,
,![]() ,此时五边形
,此时五边形![]() 的面积记为
的面积记为![]() .将点
.将点![]() 与点
与点![]() 重合的位置作为矩形
重合的位置作为矩形![]() 平移的起点,设矩形
平移的起点,设矩形![]() 平移的长度为
平移的长度为![]() .
.
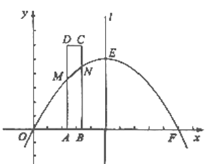
(1)求出这条抛物线的表达式;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)当矩形![]() 沿着
沿着![]() 轴的正方向平移时,求
轴的正方向平移时,求![]() 关于
关于![]() 的函数表达式,并求出
的函数表达式,并求出![]() 为何值时,
为何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
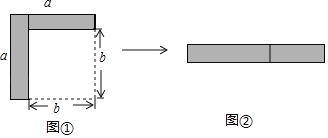
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2018根火柴棍,并且正三角形的个数比正六边形的个数多7个,那么能连续搭建正三角形的个数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个边长分别为a,b的正方形.
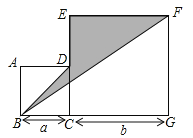
(1)用含a,b的代数式表示三角形BGF的面积;(2)当![]() ,
,![]() 时,求阴影部分的面积.
时,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
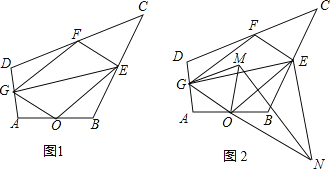
【题目】如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.
①若OE=![]() ,OG=1,求
,OG=1,求![]() 的值;
的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工分别住在![]() 三个住宅区,
三个住宅区,![]() 区有
区有![]() 人,
人,![]() 区有
区有![]() 人,
人,![]() 区有
区有![]() 人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )
人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )

A.![]() 区B.
区B.![]() 区C.
区C.![]() 区D.不确定
区D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com