
【题目】如图,BD为四边形ABCD的对角线,BC=AD,∠A=∠CBD,∠ABD=120°,AB=3,CD=![]() ,则BC的长为_____________.
,则BC的长为_____________.
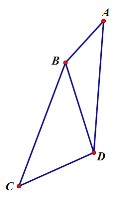
【答案】7
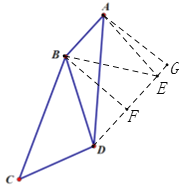
【解析】如图,过点D作DE//BA,并且使DE=BD,连接BE,AE,过点B作BF⊥DE于点F,过点A作AG⊥DE于点G,则四边形ABFG是矩形,从而有FG=AB=3,AG=BF,通过证明△ADE≌△CBD,可得AE=CD=![]() ,根据已知易得△BDE是等边三角形,根据等边三角形的性质可得DF=
,根据已知易得△BDE是等边三角形,根据等边三角形的性质可得DF=![]() BD,BF=
BD,BF=![]() BD,在Rt△AEG中,利用勾股定理可求得BD=5,从而得AG=
BD,在Rt△AEG中,利用勾股定理可求得BD=5,从而得AG=![]() ,DG=
,DG=![]() ,在Rt△ADG中,根据勾股定理求得AD长即可得答案.
,在Rt△ADG中,根据勾股定理求得AD长即可得答案.
如图,过点D作DE//BA,并且使DE=BD,连接BE,AE,过点B作BF⊥DE于点F,过点A作AG⊥DE于点G,则四边形ABFG是矩形,
∴FG=AB=3,AG=BF,
∵AB//DE,∴∠ADE=∠BAD,
∵∠BAD=∠CBD,
∴∠ADE=∠CBD,
又∵DE=BD,AD=BC,
∴△ADE≌△CBD,
∴AE=CD=![]() ,
,
∵∠ABD=120°,DE//AB,
∴∠BDE=60°,
∴△BDE是等边三角形,
∴DF=![]() BD,BF=
BD,BF=![]() BD,
BD,
在Rt△AEG中, AE2=AG2+EG2,EG=DF+FG-DE=![]() BD+3-BD=3-
BD+3-BD=3-![]() BD,
BD,
∴![]() ,
,
∴BD=5或BD=-2(舍去),
∴AG=![]() ,DG=DF+FG=
,DG=DF+FG=![]() +3=
+3=![]() ,
,
在Rt△ADG中,AD2=AG2+DG2=(![]() )2+(
)2+(![]() )2=49,
)2=49,
∴AD=7,
∴BC=7,
故答案为:7.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】八(6)班为从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评.其中,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表;另全班50位同学参与民主测评进行投票,结果如下图:
![]()
A | B | C | D | E | |
甲 | 89 | 91 | 92 | 94 | 93 |
乙 | 90 | 86 | 85 | 91 | 94 |

规定: 演讲得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两位选手各自演讲答辩的平均分;
(2)民主测评统计图中a= ,b= ;
(3)求甲、乙两位选手的民主测评得分;
(4)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,那么下列条件中不能判定四边形
,那么下列条件中不能判定四边形![]() 是菱形的为( )
是菱形的为( )
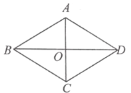
A. ∠OAB=∠OBAB. ∠OBA=∠OBCC. AD∥BCD. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:将矩形纸片ABCD折叠,使点A与点C重合(点D与D'为对应点),折痕为EF,连接AF.
(1)如图1,求证:四边形AECF为菱形;
(2)如图2,若FC=2DF,连接AC交EF于点O,连接DO、D'O,在不添加任何辅助线的情况下,请直接写出图2中所有等边三角形.
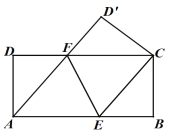

(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 于点
于点![]() ,连
,连![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ..其中正确结论的个数为( )
..其中正确结论的个数为( )

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)[(-3a2b3)3]2;
(2)(-2xy2)6+(-3x2y4)3;
(3)![]() ;
;
(4)(0.5×3![]() )199×(-2×
)199×(-2×![]() )200.
)200.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com