
【题目】如图,抛物线经过原点O(0,0),点A(1,1),点B(![]() ,0).
,0).
(1)求抛物线解析式;
(2)连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积;
(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似,若存在,求出点M的坐标;若不存在,说明理由.

【答案】(1)![]() ;(2)4;(3)(
;(2)4;(3)(![]() ,﹣54)或(
,﹣54)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )
)
【解析】
(1)设交点式y=ax(x-![]() ),然后把A点坐标代入求出a即可得到抛物线解析式;
),然后把A点坐标代入求出a即可得到抛物线解析式;
(2)延长CA交y轴于D,如图1,易得OA=![]() ,∠DOA=45°,则可判断△AOD为等腰直角三角形,所以OD=
,∠DOA=45°,则可判断△AOD为等腰直角三角形,所以OD=![]() OA=2,则D(0,2),利用待定系数法求出直线AD的解析式为y=-x+2,再解方程组
OA=2,则D(0,2),利用待定系数法求出直线AD的解析式为y=-x+2,再解方程组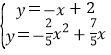 ,得C(5,-3),然后利用三角形面积公式,利用S△AOC=S△COD-S△AOD进行计算;
,得C(5,-3),然后利用三角形面积公式,利用S△AOC=S△COD-S△AOD进行计算;
(3)如图2,作MH⊥x轴于H,AC=4![]() ,OA=
,OA=![]() ,设M(x,-
,设M(x,-![]() x2+
x2+![]() x)(x>0),根据三角形相似的判定,由于∠OHM=∠OAC,则当
x)(x>0),根据三角形相似的判定,由于∠OHM=∠OAC,则当![]() 时,△OHM∽△OAC,即
时,△OHM∽△OAC,即![]() ;当
;当![]() 时,△OHM∽△CAO,即
时,△OHM∽△CAO,即![]() ,则分别解关于x的绝对值方程可得到对应M点的坐标,由于△OMH∽△ONM,所以求得的M点能以点O,M,N为顶点的三角形与(2)中的△AOC相似.
,则分别解关于x的绝对值方程可得到对应M点的坐标,由于△OMH∽△ONM,所以求得的M点能以点O,M,N为顶点的三角形与(2)中的△AOC相似.
(1)设抛物线解析式为y=ax(x-![]() ),
),
把A(1,1)代入得a1(1-![]() )=1,解得a=-
)=1,解得a=-![]() ,
,
∴抛物线解析式为y=-![]() x(x-
x(x-![]() ),
),
即y=-![]() x2+
x2+![]() x;
x;
(2)延长CA交y轴于D,如图1,
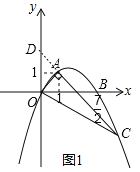
∵A(1,1),
∴OA=![]() ,∠DOA=45°,
,∠DOA=45°,
∴△AOD为等腰直角三角形,
∵OA⊥AC,
∴OD=![]() OA=2,
OA=2,
∴D(0,2),
易得直线AD的解析式为y=-x+2,
解方程组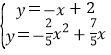 得
得![]() 或
或![]() ,则C(5,-3),
,则C(5,-3),
∴S△AOC=S△COD-S△AOD=![]() ×2×5-
×2×5-![]() ×2×1=4;
×2×1=4;
(3)存在.如图2,
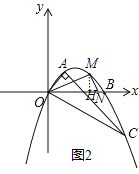
作MH⊥x轴于H,AC=![]() ,OA=
,OA=![]() ,
,
设M(x,-![]() x2+
x2+![]() x)(x>0),
x)(x>0),
∵∠OHM=∠OAC,
∴当![]() 时,△OHM∽△OAC,即
时,△OHM∽△OAC,即![]() ,
,
解方程-![]() x2+
x2+![]() x =4x得x1=0(舍去),x2=-
x =4x得x1=0(舍去),x2=-![]() (舍去),
(舍去),
解方程-![]() x2+
x2+![]() x =-4x得x1=0(舍去),x2=
x =-4x得x1=0(舍去),x2=![]() ,此时M点坐标为(
,此时M点坐标为(![]() ,-54);
,-54);
当![]() 时,△OHM∽△CAO,即
时,△OHM∽△CAO,即![]() ,
,
解方程-![]() x2+
x2+![]() x=
x=![]() x得x1=0(舍去),x2=
x得x1=0(舍去),x2=![]() ,此时M点的坐标为(
,此时M点的坐标为(![]() ,
,![]() ),
),
解方程-![]() x2+
x2+![]() x=-
x=-![]() x得x1=0(舍去),x2=
x得x1=0(舍去),x2=![]() ,此时M点坐标为(
,此时M点坐标为(![]() ,-
,-![]() );
);
∵MN⊥OM,
∴∠OMN=90°,
∴∠MON=∠HOM,
∴△OMH∽△ONM,
∴当M点的坐标为(![]() ,-54)或(
,-54)或(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() )时,以点O,M,N为顶点的三角形与(2)中的△AOC相似.
)时,以点O,M,N为顶点的三角形与(2)中的△AOC相似.


科目:初中数学 来源: 题型:
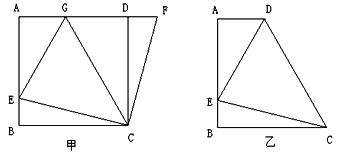
【题目】如图(甲),在正方形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() ;
;
(2)在如图(甲)中,若![]() 在
在![]() 上,且
上,且![]() ,则
,则![]() 成立吗?
成立吗?
证明你的结论.(3)运用(1)(2)解答中积累的经验和知识,完成下题:
如图(乙)四边形![]() 中,
中,![]() ∥
∥![]() (
(![]() >
>![]() ),
),![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴,y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求此时反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠ACB=90°,AC=BC,直线l经过点C,BD⊥l,AE⊥l,,垂足分别为D、E.
(1)当A、B在直线l同侧时,如图1,
①证明:△AEC≌△CDB;
②若AE=3,BD=4,计算△ACB的面积.(提示:间接求)
(2)当A. B在直线l两侧时,如图2,若AE=3,BD=4,连接AD,BE直接写出梯形ADBE的面积___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:将矩形纸片ABCD折叠,使点A与点C重合(点D与D'为对应点),折痕为EF,连接AF.
(1)如图1,求证:四边形AECF为菱形;
(2)如图2,若FC=2DF,连接AC交EF于点O,连接DO、D'O,在不添加任何辅助线的情况下,请直接写出图2中所有等边三角形.
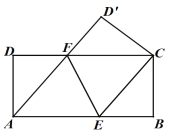

(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题;
(1)4(a3)4﹣(3a6)2
(2)﹣6xy(x﹣2y)
(3)(9x2y﹣6xy2)÷3xy
(4)(a+2b)(a﹣2b)﹣(a+b)2
(5)(﹣12)0+2﹣2
(6)20182﹣2017×2019(用公式)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com