
【题目】矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴,y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求此时反比例函数的解析式.

【答案】(1)E(2,3);(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)先确定出点C坐标,进而得出点F坐标,即可得出结论;
(2)先确定出点F的横坐标,进而表示出点F的坐标,得出CF,同理表示出CF,即可得出结论;
(3)先判断出△EHG∽△GBF,即可求出BG,最后用勾股定理求出k,即可得出结论.
(1)∵OA=3,OB=4,
∴B(4,0),C(4,3),
∵F是BC的中点,
∴F(4,![]() ),
),
∵F在反比例y=![]() 函数图象上,
函数图象上,
∴k=4×![]() =6,
=6,
∴反比例函数的解析式为y=![]() ,
,
∵E点的坐标为3,
∴E(2,3);
(2)∵F点的横坐标为4,
∴F(4,![]() ),
),
∴CF=BC﹣BF=3﹣![]() =
=![]()
∵E的纵坐标为3,
∴E(![]() ,3),
,3),
∴CE=AC﹣AE=4﹣![]() =
=![]() ,
,
在Rt△CEF中,tan∠EFC=![]() ,
,
(3)如图,由(2)知,CF=![]() ,CE=
,CE=![]() ,
,![]() ,
,
过点E作EH⊥OB于H,
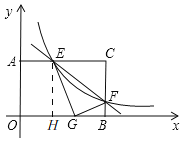
∴EH=OA=3,∠EHG=∠GBF=90°,
∴∠EGH+∠HEG=90°,
由折叠知,EG=CE,FG=CF,∠EGF=∠C=90°,
∴∠EGH+∠BGF=90°,
∴∠HEG=∠BGF,
∵∠EHG=∠GBF=90°,
∴△EHG∽△GBF,
∴![]() ,
,
∴![]() ,
,
∴BG=![]() ,
,
在Rt△FBG中,FG2﹣BF2=BG2,
∴(![]() )2﹣(
)2﹣(![]() )2=
)2=![]() ,
,
∴k=![]() ,
,
∴反比例函数解析式为y=![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
【题目】冰封文教店用1200元购进了甲、乙两种钢笔,已知甲种钢笔进价为每支12元,乙种钢笔进价为每支10元。在销售时甲种钢笔售价为每支15元,乙种钢笔售价为每支12元,全部售完后共获利270元。
(1)求冰封文教店购进甲、乙两种钢笔各多少支?
(2)冰封文教店以原价再次购进甲、乙两种钢笔,且购进甲种钢笔的数量不变,而购进乙种钢笔的数量是第一次的2倍,乙种钢笔按原售价销售,而甲种钢笔降价销售,当两种钢笔销售完毕时,要使再次购进的钢笔获利不少于340元,甲种钢笔每支最低售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂第一车间有![]() 人,第二车间比第一车间人数的
人,第二车间比第一车间人数的![]() 少30人,如果从第二车间调出10人到第一车间,那么:
少30人,如果从第二车间调出10人到第一车间,那么:
(1)两个车间共有______人?
(2)调动后,第一车间的人数为______人,第二车的人数为______人.
(3)求调动后,第一车间的人数比第二车的人数多几人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过原点O(0,0),点A(1,1),点B(![]() ,0).
,0).
(1)求抛物线解析式;
(2)连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积;
(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似,若存在,求出点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十一黄金周某一天,甲、乙两名学生去距家36千米的风景区游玩,他们从家出发,骑电动车行驶20分钟时发现忘带相机,甲下车步行前往,乙骑电动车按原路返回,乙取到相机后(在家取相机所用时间忽略不计),骑电动车追甲,在距风景区13.5千米处追上甲并同车前往风景区,若电动车速度始终不变.设甲与家相距![]() (千米),乙与家相距
(千米),乙与家相距![]() (千米),甲离开家的时间为
(千米),甲离开家的时间为![]() (分钟),
(分钟),![]() 、
、![]() 与x之间的函数图象如图所示,结合图象解答下列问题:
与x之间的函数图象如图所示,结合图象解答下列问题:

(1)求电动车的速度;
(2)求出甲步行的时间是多少分钟?;
(3)求乙返回到家时,甲与家相距多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市盘山、黄崖关长城、航母公园三景区是人们节假日游玩的热点景区.某中学对七年级(1)班学生今年暑假到这三景区游玩的计划做了全面调查,调查分四个类别,A游三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩.根据调查的结果绘制了不完全的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
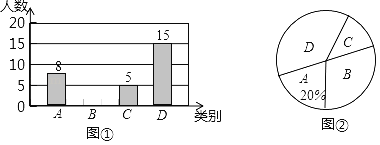
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生520人,求计划暑假选择A、B、C三个类别出去游玩的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com