【题目】计算
（1）
；
（2）
；
（3）2x 5y3x 2 y 2x x 3y；
（4）（x+1）2（x-1）2（x2+1）2．
【答案】（1）1；（2）-14x4y2+21x3y4-7x3y2；（3）4x2+17xy-10y2；（4）x8-2x4+1.
【解析】
（1）根据负整数指数幂、零指数幂即可解答本题；
（2）直接利用单项式乘以多项式运算法则计算得出答案．
（3）根据单项式乘多项式，多项式乘多项式的法则计算即可．
（4）先运用平方差公式，再利用完全平方公式即可解答.
（1）
=
=
=1.
（2）（-7x2y）（2x2y-3xy3+xy）
=-14x4y2+21x3y4-7x3y2．
（3）原式=6x2+11xy-10y2-2x2+6xy，
=4x2+17xy-10y2．
（4）原式=[(x+1)(x-1)]2(x2+1) 2=(x2-1) 2 (x2+1) 2=[(x2-1)(x2+1)] 2=(x4-1) 2=x8-2x4+1.
全能闯关100分系列答案科目：初中数学 来源： 题型：
【题目】定义：若点P为四边形ABCD内一点，且满足∠APB+∠CPD=180°， 则称点P为四边形ABCD的一个“互补点”．
（1）如图1，点P为四边形ABCD的一个“互补点”，∠APD=63°，求∠BPC的度数．
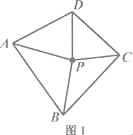
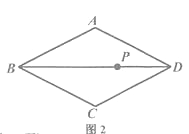
（2）如图2，点P是菱形ABCD对角线上的任意一点．求证：点P为菱形ABCD的一个“互补点”．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，AD∥BC，AD=5，B（-3，0），C（9，0），点E是BC的中点，点P是线段BC上一动点，当PB=________时，以点P、A、D、E为顶点的四边形是平行四边形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为打造书香校园，计划购进甲乙两种规格的书柜放置新购置的图书，调查发现，若购买甲种书柜3个，乙种书柜2个，共需要资金1020元；若购买甲种书柜4个，乙种书柜3个，共需资金1440元.
（1）甲乙两种书柜每个的价格分别是多少元？
（2）若该校计划购进这两种规格的书柜共20个（其中乙种书柜的数量不少于甲种书柜的数量的
）.设该校计划购进甲种书柜m个，资金总额为W元.求W与m的函数关系式,并请你为该校设计资金最少的购买方案.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠C=90°，AC=2，BC=5，点D是BC边上一点且CD=1，点P是线段DB上一动点，连接AP，以AP为斜边在AP的下方作等腰Rt△AOP．当P从点D出发运动至点B停止时，点O的运动路径长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某慈善组织租用甲、乙两种货车共
辆，把蔬菜
吨，水果
吨，全部运到灾区已知辆甲种货车同时可装蔬菜
吨，水果
吨；一辆乙种货车同时可装蔬菜吨，水果
吨.
(1)若将这批货物一次性运到灾区，请写出具体的租车方案？
(2)若甲种货车每辆需付燃油费
元，乙种货车每辆需付燃油费
元，则应选(1)种的哪种方案，才能使所付的燃油费最少？最少的燃油费是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F的反比例函数y=
（k＞0）的图象与边AC交于点E．
（1）当点F运动到边BC的中点时，求点E的坐标；
（2）连接EF，求∠EFC的正切值；
（3）如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC中，∠ACB＝90°，AC＝BC，直线l经过点C，BD⊥l，AE⊥l，，垂足分别为D、E．
（1）当A、B在直线l同侧时，如图1，
①证明：△AEC≌△CDB；
②若AE=3,BD=4,计算△ACB的面积.(提示：间接求)
(2)当A. B在直线l两侧时，如图2，若AE=3，BD=4，连接AD，BE直接写出梯形ADBE的面积___.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
中，
，小聪同学利用直尺和圆规完成了如下操作：
①作
的平分线
交
于点
；
②作边
的垂直平分线
，与相交于点
；
③连接
，
.
请你观察图形解答下列问题：
（1）线段
，，之间的数量关系是________；
（2）若
，求
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com