
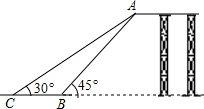
 如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.
如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离. 分析 根据AB长为4米,∠ABD=45°,求出AD、BD的长度,然后根据∠ACD=30°求出AC、CD的长度,由BC=CD-BD求出BC.
解答 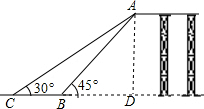 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,
在Rt△ABD中,AB=4,∠ABD=45°,
∵sin∠ABD=$\frac{AD}{AB}$,
∴AD=AB•sin45°=$4×\frac{\sqrt{2}}{2}$=2$\sqrt{2}$(米),
∴BD=AD=2$\sqrt{2}$(米),
在Rt△ACD中,∠ACD=30°
∵sin$∠ACD=\frac{AD}{AC}$,
∴AC=$\frac{AD}{sin30°}$=$\frac{2\sqrt{2}}{\frac{1}{2}}$=4$\sqrt{2}$(米),
∴CD=$\sqrt{{AC}^{2}{-AD}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{6}$(米),
∴BC=CD-BD=2$\sqrt{6}$-2$\sqrt{2}$=2($\sqrt{6}$-$\sqrt{2}$)(米).
答:改造后滑梯AC的长为4$\sqrt{2}$米,新、旧滑梯着地点C、B之间的距离为2($\sqrt{6}$-$\sqrt{2}$)米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数的知识求解.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
| A. | p<m<n<q | B. | m<p<q<n | C. | m<p<n<q | D. | p<m<q<n |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
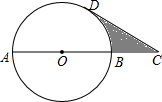 如图,AB为⊙O的直径,点C在AB的延长线上,且AB=2BC=4,CD与⊙O相切于点D,则图中阴影部分的面积是2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)
如图,AB为⊙O的直径,点C在AB的延长线上,且AB=2BC=4,CD与⊙O相切于点D,则图中阴影部分的面积是2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
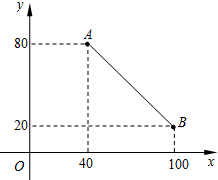 如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.
如图,线段AB表示一种产品的销售量y(吨)与销售价格x(元/吨)之间的对应关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com