
����Ŀ����ͼ��1����������ȫ�ȵ�ֱ�������Σ�ֱ�DZ߷ֱ�Ϊa��b��б��Ϊc��
��1�������������������ι������ͼ��2����ͼ�Σ��������ͼ�Σ�֤����a2+b2��c2��
��2�������������������ι���ͼ3��ͼ�Σ������������ͼ��֤�����⣨1���Ľ���������ܣ���д��֤�����̣�
��3����a��3��b��4ʱ��������һ��ֱ�������η���ƽ��ֱ������ϵ�У�ʹֱ�Ƕ�����ԭ���غϣ���ֱ�DZ�a��b�ֱ���x�ᡢy���غϣ���ͼ4��Rt��AOB��λ�ã�����CΪ�߶�OA��һ�㣬����ABC����ֱ��BC���ۣ���Aǡ������x���ϵ�D����
����д��C��D��������ꣻ
������CMDΪ���������Σ���M��x���ϣ���ֱ��д���������������е�M�����꣮
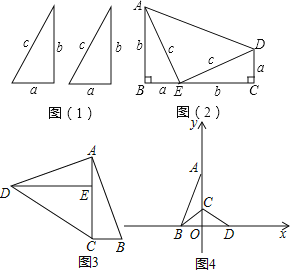
���𰸡���1������������2���ܣ�����������3����C��D���������ΪC��0��![]() ����D��2��0�����ڷ������������е�M������Ϊ����
����D��2��0�����ڷ������������е�M������Ϊ����![]() ��0������
��0������![]() ��0����������2��0��������
��0����������2��0��������![]() ��0��
��0��
��������
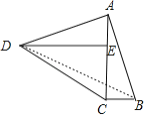
��1���������ε���������ֱ�ʾ��������֤����
��2�������ı���ABCD����������ֱ�ʾ��������֤����
��3���ٸ��ݷ��۵����ʺ��ɶ���������⣻
�ڸ��ݵ��������ε����ʷ����������⼴�ɣ�
�⣺��1����S����ABCD=![]()
S����ABCD=![]()
![]()
![]()
![]() ��
��
��2������![]() ��
��
��ͼ��
S�ı���ABCD=![]() ��
��
S�ı���ABCD=![]() ��
��
![]()
![]() ��
��
![]() ��
��
��3������![]() ����
����![]() ����
����![]() ��
��
���ݷ��ۿ�֪��
![]() ��
��![]() ��
��
![]() ��
��
��![]() �У����ݹ��ɶ�������
�У����ݹ��ɶ�������
![]() ��
��
���![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��![]() ���������Ϊ
���������Ϊ![]() ��
��![]() ��
��
����ͼ��
����![]() ��
��![]() ����������ʱ��
����������ʱ��
![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
����![]() ��
��![]() �Ḻ������ʱ��
�Ḻ������ʱ��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
��������������е�![]() ������Ϊ��
��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
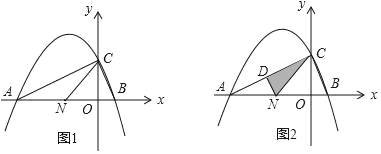
����Ŀ����ͼ1��������y=��![]() x2+bx+c��a��0����x�ύ��A����4��0����B��1��0�����㣬��y�ύ��C�㣬�Գ���x=��
x2+bx+c��a��0����x�ύ��A����4��0����B��1��0�����㣬��y�ύ��C�㣬�Գ���x=��![]() ����N��n��0�����߶�AB�ϵ�һ�����㣨N��A��B���㲻�غϣ�����ش��������⣺
����N��n��0�����߶�AB�ϵ�һ�����㣨N��A��B���㲻�غϣ�����ش��������⣺
��1����������ߵĽ���ʽ����д��C������ꣻ
��2���������nΪ��ֵʱ����ANCǡ�ܹ����ǵ��������Σ�
��3����ͼ2����N��NF��BC����AC�ཻ��D�㣬����CN��������N����˶������У���CDN������Ƿ�������ֵ�������ڣ�����������������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��k��0���뷴��������y=![]() ��m��0����ͼ���ڵ�һ�����ڽ���A��1��6����B��3��n�����㣮
��m��0����ͼ���ڵ�һ�����ڽ���A��1��6����B��3��n�����㣮
��1���������������ı���ʽ��
��2������ͼ��ֱ��д��kx+b��![]() ��0��x��ȡֵ��Χ��
��0��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ڼס��Ҳֿ���ij��ԭ��450�֣�����˳��ײֿ�����ԭ�ϵ�60%���Ҳֿ�����ԭ�ϵ�40%����ô�Ҳֿ�ʣ���ԭ�ϱȼײֿ�ʣ���ԭ�϶�30�֣�
��1����ס������ֿ�����ԭ�϶��ٶ֣�
��2���ֹ�˾�轫300��ԭ�������������Ӽס��������ֿ�������˼۷ֱ�Ϊ120Ԫ/�ֺ�100Ԫ/�֣���Э�̣��Ӽײֿ�������˼ۿ��Ż�aԪ�֣�10��a��30�������Ҳֿ�������˼۲��䣬��Ӽײֿ���m��ԭ�ϵ���������������˷�W����m�ĺ�������ʽ����Ҫ��д��m��ȡֵ��Χ����
��3���ڣ�2���������£�����ݺ���������˵��������m������W�ı仯�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
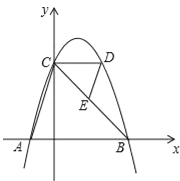
����Ŀ����ͼ��������y=����x��1��2+4��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��CD��x�ύ����������һ��D������AC��DE��AC����CB�ڵ�E��
��1����A��B��������ꣻ
��2������CDE����BAC�����֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
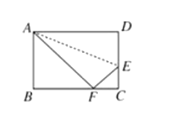
����Ŀ����ͼ���۵�������![]() ��ʹ����
��ʹ����![]() ��
��![]() ���ϵĵ�
���ϵĵ�![]() �غϣ���֪������
�غϣ���֪������![]() �ij���Ϊ
�ij���Ϊ![]() ����Ϊ
����Ϊ![]() ����
����![]() ______��
______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ��Ƴ���������ͳ��ͼ��
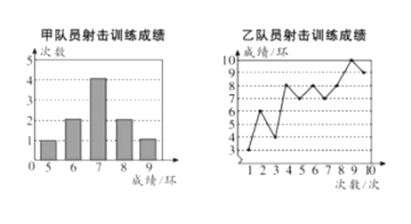
����������Ϣ�����������������£�
ƽ���������� | ��λ�������� | ���������� | ���� | |
�� |
|
|
|
|
�� |
|
|
|
|
��1��������![]() ��
��![]() ��
��![]() ��
��
��2���ֱ����ñ��е��ĸ�ͳ��������Ҫ������������Ա�����ѵ���ɼ�����ѡ������һ������������ΪӦѡ������Ա��
��3������������![]() ������
�Σ�����![]() ������ô�ҵ�����ɼ��ķ��� ����������С�����䡱��
������ô�ҵ�����ɼ��ķ��� ����������С�����䡱��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
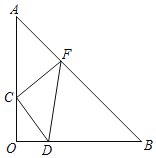
����Ŀ����ͼ����AOB�У���AOB��90����OA��OB������ֱ����CDF��ֱ�Ƕ���C�ڱ�OA�ϣ���D�ڱ�OB�ϣ���F�ڱ�AB�ϣ������CDF���������AOB�������![]() ��OD��2������AOB�����Ϊ____��
��OD��2������AOB�����Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
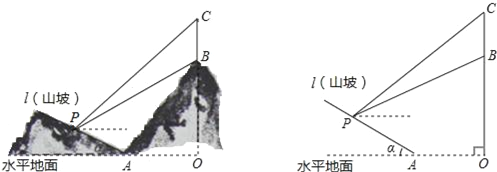
����Ŀ����ͼ��ʾ��ij���̶�����ɽ�£�ɽ����Ϊֱ��l������һ��·����Ҫ����ɽ�µ��¶ȣ���tan����ֵ������Ա��ɽ��P�������ƴ������ߣ��۲����ɽ���ϵ�һ���������������C������Ϊ31�㣬����B������Ϊ26.6�㣮��֪����BC=40�ף������ڵ�ɽ��OB=240�ף�OA=300�ף�ͼ�еĵ�O��B��C��A��P��ͬһƽ���ڣ�
��
��1��P��OC�ľ��룮
��2��ɽ�µ��¶�tan����
�������sin26.6���0.45��tan26.6���0.50��sin31���0.52��tan31���0.60��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com