
����Ŀ����һԪ���η����У���������Τ�ﶨ��������һԪ���η���![]() ���������������ʵ����
���������������ʵ����![]() ����ô
����ô![]() ��˵������������������
��˵������������������![]() �������緽��
�������緽��![]() �У�
�У�![]() �����Ը÷������������ȵ�ʵ�������Ƿ��̵�����Ϊ
�����Ը÷������������ȵ�ʵ�������Ƿ��̵�����Ϊ![]() ��
��![]() ����ô
����ô![]() +
+![]() =
=![]() ��
��![]()
![]() =
=![]() ,������Ķ����Ͻ�����и��⣺
,������Ķ����Ͻ�����и��⣺
��1����֪����![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() >
>![]() ,�����и�ʽ��ֵ:
,�����и�ʽ��ֵ:
��![]() ��
��![]()
��2����֪![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������
������ʵ������
���Ƿ����ʵ��![]() ��ʹ
��ʹ![]() �����������ڣ����
�����������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
����ʹ![]() ��ֵΪ������ʵ��
��ֵΪ������ʵ��![]() ������ֵ��
������ֵ��
���𰸡���1����13��-![]() ��2���ٲ����ڢ�-2,-3��-5
��2���ٲ����ڢ�-2,-3��-5
��������
��1�����ݸ���ϵ���Ĺ�ϵ���![]() +
+![]() ��
��![]() ��ֵ���Ѣ��䷽���Ѣ�ͨ�֣�Ȼ���
��ֵ���Ѣ��䷽���Ѣ�ͨ�֣�Ȼ���![]() +
+![]() ��
��![]() ��ֵ������㼴�ɣ�
��ֵ������㼴�ɣ�
��2�����ݷ���������ʵ���������![]() +
+![]() ��
��![]() ��ֵ����
��ֵ����![]() ��ȡֵ��Χ���ٰ�����ʽ�ӻ������룬��
��ȡֵ��Χ���ٰ�����ʽ�ӻ������룬��![]() +
+![]() ��
��![]() ��ֵ���룬�������
��ֵ���룬�������![]() ��ֵ����ͨ�ֺ�
��ֵ����ͨ�ֺ�![]() +
+![]() ��
��![]() ��ֵ���룬���ۼ���.
��ֵ���룬���ۼ���.
��1���߷���![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() >
>![]() ��
��
��![]() =3 ��
=3 �� ![]() =-2 ��
=-2 ��
��![]() =
=![]() =9+4=13��
=9+4=13��
![]() =
=![]() ��
��
��2����![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������
������ʵ������
��![]() �� ��k<0��
�� ��k<0��
![]() =1 ,
=1 , ![]() =
=![]() ��
��
�������������ʵ��k.��![]()
=![]() ��
��
��� ![]() ��
��
��k<0 �� �����������ʵ��k ��
��![]()
=![]()
=-![]() ��
��
Ҫʹ-![]() Ϊ���� �� ��
���� �� ��![]() ��
��
��k=0,-2,1,-3,-5,3 ��
�֡�k<0 �� ��k=-2,-3��-5.


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ��
��ͼ��![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��ֱ�ߡ�
��ֱ�ߡ�
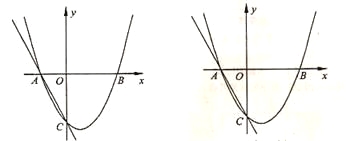
��1������κ����Ľ���ʽ��
��2����![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ����
����![]() �ij���
�ij���
��3����![]() �ڶ��κ���ͼ���ϣ���
�ڶ��κ���ͼ���ϣ���![]() ΪԲ�ĵ�Բ��ֱ��
ΪԲ�ĵ�Բ��ֱ��![]() ���У��е�Ϊ
���У��е�Ϊ![]() ��
��
�� ��![]() ��
��![]() ���Ҳ࣬��
���Ҳ࣬��![]() ����
����![]() ���
���![]() ��Ӧ�������
��Ӧ�������![]() �����ꣻ
�����ꣻ
�� ��![]() �İ뾶Ϊ
�İ뾶Ϊ![]() �����
�����![]() �����ꡣ
�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
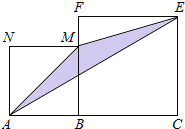
����Ŀ����ͼ���߶�AC=n+1������nΪ������������B���߶�AC�ϣ����߶�ACͬ����������ABMN��������BCEF������AM��ME��EA�õ���AME����AB=1ʱ����AME�������ΪS1����AB=2ʱ����AME�������ΪS2����AB=3ʱ����AME�������Ϊ
S3����S3��S2= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
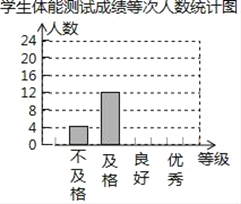
����Ŀ��ijУΪ�˽�ѧ������������Ӹ��꼶�����ȡ����ѧ���������ܲ��ԣ�ÿ��ѧ���IJ��Գɼ�������ӦΪ���㡢���á����������ĸ��ȼ���ͳ��Ա�ڽ��������ݻ��Ƴ�ͼ��ʱ���֣�����©ͳ��4�ˣ�����©ͳ��6�ˣ����Ǽ�ʱ�������Ӷ��γ���ͼͼ�����밴��ȷ���ݽ�����и��⣺
ѧ�����ܲ��Գɼ����ȴ�����ͳ�Ʊ�
���ܵȼ� | ����ǰ���� | ���������� |
���� | 8 | �� �� |
���� | 16 | �� �� |
���� | 12 | �� �� |
������ | 4 | �� �� |
�ϼ� | 40 | �� �� |
��1����дͳ�Ʊ���
��2�����ݵ��������ݣ���ȫ����ͳ��ͼ��
��3������У����ѧ��1500�ˣ�����������У���ܲ��Եȼ�Ϊ����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�ڶ����ÿ�չ���ܵ���ѧ��������ѧ�ڽ�����Բ���ѧ������һ�Ρ�����ϲ���ĵڶ����á��ʾ����飨ÿ��ѧ�������˵��˱�����ֻѡ��һ����Ŀ����ͳ�ƺ�Ȥζ��ѧ���ݽ���ڲš���Ϣ�������ֹ�������������������ѡ��Ϣ������������ѡ�ֹ���������8�ˣ�ѡȤζ��ѧ������������ѡ�ֹ��������˶࣬��Ϊ��������ѡȤζ��ѧ��ѡ�ֹ�����������֮����ѡ�ݽ���ڲ���ѡ��Ϣ����������֮�͵�5����ѡȤζ��ѧ��ѡ�ݽ���ڲŵ�����֮�ͱ�ѡ��Ϣ������ѡ�ֹ�����������֮�Ͷ�24�ˣ���μӵ����ʾ���ѧ����________�ˡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1=��x��1��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B���뷴��������![]() ͼ���һ������ΪM����2��m����
ͼ���һ������ΪM����2��m����
��1�����������Ľ���ʽ����2�����B��ֱ��OM�ľ��룮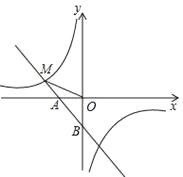
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������5�֣���ͼ��С���ڴ�¥30��
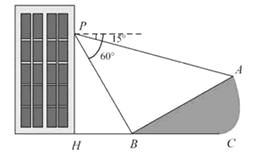
����PH��30�ף��Ĵ���P�����й۲⣬���ɽ
����A���ĸ���Ϊ15����ɽ��B���ĸ���Ϊ
60������֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��
![]() ����P��H��B��C��A��ͬһ��ƽ���ϣ���
����P��H��B��C��A��ͬһ��ƽ���ϣ���
H��B��C��ͬһ��ֱ���ϣ���PH��HC��
(1)ɽ���½ǣ�����ABC���Ķ������� �� �ȣ�
(2)��A��B�����ľ��루�����ȷ��0.1�ף��ο����ݣ�![]() ��1.732����
��1.732����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB=AC=4cm����B=30������P�ӵ�B��������![]() cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B��������1cm/s���ٶ���BA��AC�����˶�����Cֹͣ������BPQ�����Ϊy��cm2�����˶�ʱ��Ϊx��s�������������ܷ�ӳy��x֮�亯����ϵ��ͼ���ǣ�������
cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B��������1cm/s���ٶ���BA��AC�����˶�����Cֹͣ������BPQ�����Ϊy��cm2�����˶�ʱ��Ϊx��s�������������ܷ�ӳy��x֮�亯����ϵ��ͼ���ǣ�������
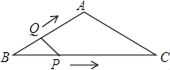
A. 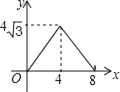 B.
B. 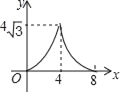
C. 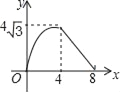 D.
D. 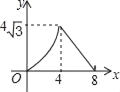
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx��3a������A����1��0����C��0��3������x�ύ����һ��B�������ߵĶ���ΪD��

��1����˶��κ�������ʽ��
��2������DC��BC��DB����֤����BCD��ֱ�������Σ�
��3���ڶԳ����Ҳ�����������Ƿ���ڵ�P��ʹ����PDCΪ���������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com