
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.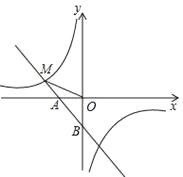
【答案】(1)![]() (2)
(2)![]()
【解析】
解:(1)∵一次函数y1=﹣x﹣1过M(﹣2,m),∴m=1。∴M(﹣2,1)。
把M(﹣2,1)代入![]() 得:k=﹣2。
得:k=﹣2。
∴反比列函数为![]() 。
。
(2)设点B到直线OM的距离为h,过M点作MC⊥y轴,垂足为C。
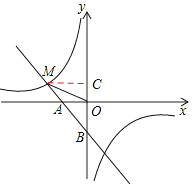
∵一次函数y1=﹣x﹣1与y轴交于点B,
∴点B的坐标是(0,﹣1)。
∴![]() 。
。
在Rt△OMC中,![]() ,
,
∵![]() ,∴
,∴![]() 。
。
∴点B到直线OM的距离为![]() .
.
(1)根据一次函数解析式求出M点的坐标,再把M点的坐标代入反比例函数解析式即可。
(2)设点B到直线OM的距离为h,过M点作MC⊥y轴,垂足为C,根据一次函数解析式表示出B点坐标,利用△OMB的面积=![]() ×BO×MC算出面积,利用勾股定理算出MO的长,再次利用三角形的面积公式可得
×BO×MC算出面积,利用勾股定理算出MO的长,再次利用三角形的面积公式可得![]() OMh,根据前面算的三角形面积可算出h的值
OMh,根据前面算的三角形面积可算出h的值


科目:初中数学 来源: 题型:
【题目】已知二元一次方程![]() ,通过列举将方程的解写成下列表格的形式:
,通过列举将方程的解写成下列表格的形式:
| -1 |
|
| 5 | 6 |
| 6 | 5 |
| 0 |
|
如果将二元一次方程的解所包含的未知数![]() 的值对应直角坐标系中一个点的横坐标,未知数
的值对应直角坐标系中一个点的横坐标,未知数![]() 的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程
的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程![]() 的解
的解![]() 的对应点是
的对应点是![]() .
.
(1)表格中的![]() ________,
________,![]() ___________;
___________;
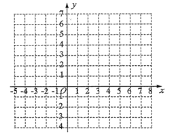
(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,并在所给的直角坐标系中画出这五个点;根据这些点猜想方程![]() 的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
(3)若点![]() 好落在
好落在![]() 的解对应的点组成的图形上,求
的解对应的点组成的图形上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
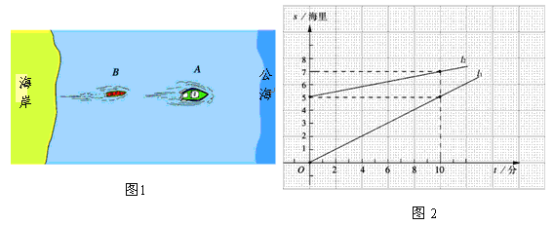
【题目】我国边防局接到情报,近海处有一可疑船只![]() 正向公海方向行驶,边防部迅速派出快艇
正向公海方向行驶,边防部迅速派出快艇![]() 追赶(如图1) .图2中
追赶(如图1) .图2中![]() 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.根据图象问答问题:
(分)之间的关系.根据图象问答问题:
(1)①直线![]() 与直线
与直线![]() 中 表示
中 表示![]() 到海岸的距离与追赶时间之间的关系;
到海岸的距离与追赶时间之间的关系;
②![]() 与
与![]() 比较 速度快;
比较 速度快;
③如果一直追下去,那么![]() ________ (填 “能”或“不能")追上
________ (填 “能”或“不能")追上![]() ;
;
④可疑船只![]() 速度是 海里/分,快艇
速度是 海里/分,快艇![]() 的速度是 海里/分;
的速度是 海里/分;
(2)![]() 与
与![]() 对应的两个一次函数表达式
对应的两个一次函数表达式![]() 与
与![]() 中
中![]() 的实际意义各是什么?并直接写出两个具体表达式.
的实际意义各是什么?并直接写出两个具体表达式.
(3)![]() 分钟内
分钟内![]() 能否追上
能否追上![]() ?为什么?
?为什么?
(4)当![]() 逃离海岸
逃离海岸![]() 海里的公海时,
海里的公海时, 将无法对其进行检查,照此速度,
将无法对其进行检查,照此速度,![]() 能否在
能否在![]() 逃入公海前将其拦截?为什么?
逃入公海前将其拦截?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,连接BD,点
边上一点,连接BD,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)在(2)的条件下,如图3,若![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 的中点,
的中点,![]() 点在射线
点在射线![]() 上,
上,![]() 点在射线
点在射线![]() 上,
上,![]() ,
,
(1)如图1,若![]() 点与点
点与点![]() 重合,求证:
重合,求证:![]() .
.
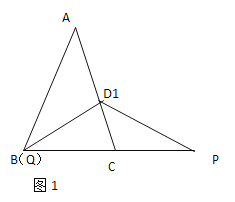
(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 求
求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
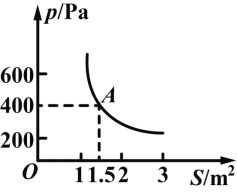
【题目】某科技小组进行野外考察,途中遇到一片十几米宽的泥地,他们沿着前进路线铺了若干块木板,构成一条临时近道,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
(1)写出这一函数的关系式和自变量的取值范围.
(2)当木板面积为0.2m2时,压强是多少?
(3)如果要求压强不超过6000Pa,那么木板的面积至少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 两点的坐标分别是点
两点的坐标分别是点![]() ,点
,点![]() ,且
,且![]() 满足:
满足:![]() .
.
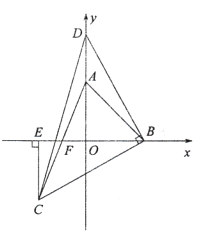
(1)求![]() 的度数;
的度数;
(2)点![]() 是
是![]() 轴正半轴上
轴正半轴上![]() 点上方一点(不与
点上方一点(不与![]() 点重合),以
点重合),以![]() 为腰作等腰
为腰作等腰![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
①求证:![]() ;
;
②连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
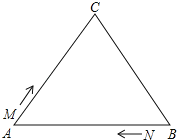
【题目】如图,![]() 中,
中,![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,
分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,![]() 、
、![]() 同时停止运动.
同时停止运动.
(1)点![]() 、
、![]() 运动几秒时,
运动几秒时,![]() 、
、![]() 两点重合?
两点重合?
(2)点![]() 、
、![]() 运动几秒时,可得到等边三角形
运动几秒时,可得到等边三角形![]() ?
?
(3)当点![]() 、
、![]() 在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时
在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时![]() 、
、![]() 运动的时间.
运动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com