
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 的中点,
的中点,![]() 点在射线
点在射线![]() 上,
上,![]() 点在射线
点在射线![]() 上,
上,![]() ,
,
(1)如图1,若![]() 点与点
点与点![]() 重合,求证:
重合,求证:![]() .
.
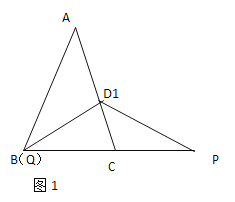
(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 求
求![]() 的值.
的值.

【答案】(1)见解析(2)12.
【解析】
(1)由等边三角形和等腰三角形的性质得出∠DBC=∠P,即可得出DB=DE;
(2)过点D作DH∥BC,交AB于点 H,证明△DQH≌△DPC(ASA),得出HQ=CP,得出BQ+BP=BH+HQ+BP=BH+BP+PC=BH+BC=![]() 即可求解.
即可求解.
(1)证明:∵△ABC 为等边三角形,
∴BA=BC,∠ABC=60![]() ,
,
∵D为AC的中点,
∴DB 平分∠ABC,
∴∠DBC=30![]() ,
,
∵![]()
∴∠P=180![]() 120
120![]() 30
30![]() =30
=30![]()
∴∠DBC=∠P,
∴DB=DP
(2)过点D作DH∥BC,交AB于点 H,如图2所示:
∵△ABC 为等边三角形,
∴∠A=∠B=∠C=60![]() ,
,
∵DH∥BC,
∴∠AHD=∠B=60![]() ,∠ADH=∠C=60
,∠ADH=∠C=60![]() ,
,
∴∠AHD=∠ADH=∠C=60![]() ,∠HDC=120
,∠HDC=120![]() ,
,
∴△ADH 是等边三角形,
∴DH=AD,
∵D为AC 的中点,
∴DA=DC,
∴DH=DC,
∵∠PDQ=120![]() ,∠HDC=120
,∠HDC=120![]() ,
,
∴∠PDH+∠QDH=∠PDH+∠CDP,
∴∠QDH=∠CDP,
在△DQH 和△DPC 中,
 ,
,
∴△DQH≌△DPC,
∴HQ=CP,
∴BQ+BP=BH+HQ+BP=BH+BP+PC=BH+BC=![]() =12,
=12,
即![]() =12.
=12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
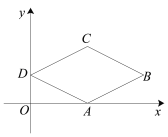
【题目】如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中B点坐标是(8,2),D点坐标是(0,2),点A在x轴上,则菱形ABCD的周长是( )
A.2![]()
B.8
C.8![]()
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、 “很强”四个层次,并绘制成如下两幅尚不完整的统计图:
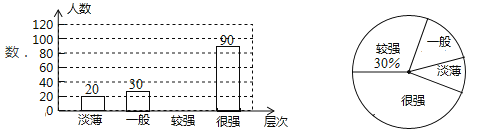
根据以上信息,解答下列问题:
(1)该校有![]() 名学生,现要对安全意识为“淡薄”、“一般"的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
名学生,现要对安全意识为“淡薄”、“一般"的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请将条形统计图补充完整.
(3)求出安全意识为“较强”的学生所占的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
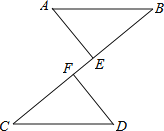
【题目】如图,AB∥CD,AB=CD,点E、F在BC上,且BF=CE.
(1)求证:△ABE≌△DCF;
(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.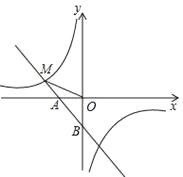
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (x>0)交于点A,将直线y1=
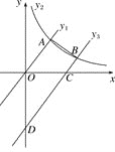
(x>0)交于点A,将直线y1=![]() x向下平移4个单位后称该直线为y3,若y3与双曲线交于B,与x轴交于C,与y轴交于D,AO=2BC,连接AB,则以下结论错误的有( )
x向下平移4个单位后称该直线为y3,若y3与双曲线交于B,与x轴交于C,与y轴交于D,AO=2BC,连接AB,则以下结论错误的有( )
①点C坐标为(3,0);②k=![]() ;③S四边形OCBA=
;③S四边形OCBA=![]() ;④当2<x<4时,有y1>y2>y3;⑤S四边形ABDO=2S△COD.
;④当2<x<4时,有y1>y2>y3;⑤S四边形ABDO=2S△COD.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
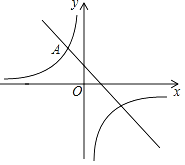
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=﹣x+1的图象的一个交点为A(﹣1,m).
的图象与一次函数y=﹣x+1的图象的一个交点为A(﹣1,m).
(1)求这个反比例函数的表达式;
(2)如果一次函数y=﹣x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y=![]() 的值的范围.
的值的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某商场有可上行和下行的两条自动扶梯,扶梯上行和下行的长度相等,运行速度相同且保持不变,甲、乙两人同时站上了上行和下行端,甲站上上行扶梯的同时又以0.8米/秒的速度往上走,乙站上下行扶梯后则站立不动随扶梯下行,甲到达扶梯顶端后立即乘坐下行扶梯(换乘时间忽略不计)同时以0.8米/秒的速度往下走,乙到达低端后则在原点等候甲,图②中线段OB、AB分别表示甲、乙两人在乘坐扶梯过程中,高扶梯底端的路程y(米)与所用时间x(秒)的部分函数图象,结合图象解答下列问题:
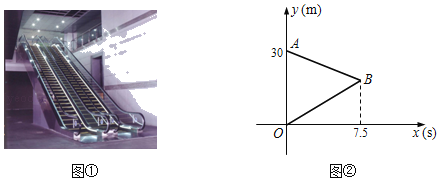
(1)每条扶梯的长度为 米(直接填空);
(2)求点B的坐标;
(3)乙到达扶梯底端后,还需等待 秒,甲才到达扶梯底端(直接填空).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com