
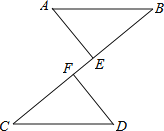
【题目】如图,AB∥CD,AB=CD,点E、F在BC上,且BF=CE.
(1)求证:△ABE≌△DCF;
(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
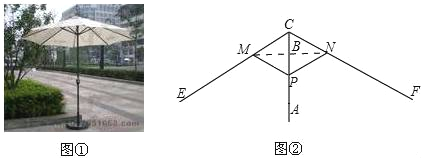
【题目】图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2、当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开、已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米、设AP=x分米.
(1)求x的取值范围;
(2)若∠CPN=60°,求x的值;
(3)设阳光直射下,伞下的阴影(假定为圆面)面积为y,求y关于x的关系式(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
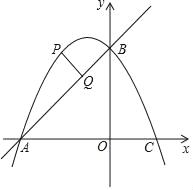
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
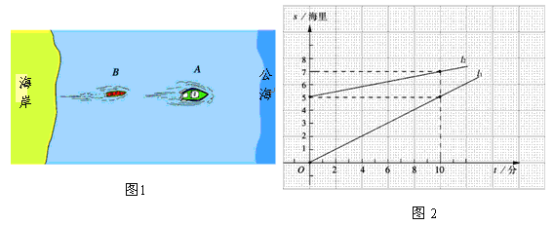
【题目】我国边防局接到情报,近海处有一可疑船只![]() 正向公海方向行驶,边防部迅速派出快艇
正向公海方向行驶,边防部迅速派出快艇![]() 追赶(如图1) .图2中
追赶(如图1) .图2中![]() 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.根据图象问答问题:
(分)之间的关系.根据图象问答问题:
(1)①直线![]() 与直线
与直线![]() 中 表示
中 表示![]() 到海岸的距离与追赶时间之间的关系;
到海岸的距离与追赶时间之间的关系;
②![]() 与
与![]() 比较 速度快;
比较 速度快;
③如果一直追下去,那么![]() ________ (填 “能”或“不能")追上
________ (填 “能”或“不能")追上![]() ;
;
④可疑船只![]() 速度是 海里/分,快艇
速度是 海里/分,快艇![]() 的速度是 海里/分;
的速度是 海里/分;
(2)![]() 与
与![]() 对应的两个一次函数表达式
对应的两个一次函数表达式![]() 与
与![]() 中
中![]() 的实际意义各是什么?并直接写出两个具体表达式.
的实际意义各是什么?并直接写出两个具体表达式.
(3)![]() 分钟内
分钟内![]() 能否追上
能否追上![]() ?为什么?
?为什么?
(4)当![]() 逃离海岸
逃离海岸![]() 海里的公海时,
海里的公海时,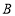 将无法对其进行检查,照此速度,
将无法对其进行检查,照此速度,![]() 能否在
能否在![]() 逃入公海前将其拦截?为什么?
逃入公海前将其拦截?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
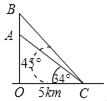
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.
(1)求A,B两点间的距离(结果精确到0.1km).
(2)当运载火箭继续直线上升到D处,雷达站测得其仰角为56°,求此时雷达站C和运载火箭D两点间的距离(结果精确到0.1km).(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 的中点,
的中点,![]() 点在射线
点在射线![]() 上,
上,![]() 点在射线
点在射线![]() 上,
上,![]() ,
,
(1)如图1,若![]() 点与点
点与点![]() 重合,求证:
重合,求证:![]() .
.
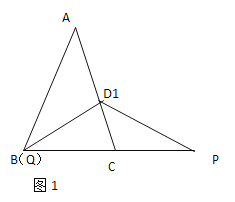
(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 求
求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用![]() 元购书若干本, 并按该书定价
元购书若干本, 并按该书定价![]() 元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了
元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了![]() ,他用
,他用![]() 元所购该书数量比第一次多
元所购该书数量比第一次多![]() 本.当按定价
本.当按定价![]() 元售出
元售出![]() 本时,出现滞销,便以定价的
本时,出现滞销,便以定价的![]() 折售完剩余的书.
折售完剩余的书.
![]() 每本书第一次的批发价是多少钱?
每本书第一次的批发价是多少钱?
![]() 试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com