
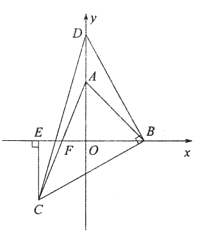
【题目】如图,在平面直角坐标系中,![]() 两点的坐标分别是点
两点的坐标分别是点![]() ,点
,点![]() ,且
,且![]() 满足:
满足:![]() .
.
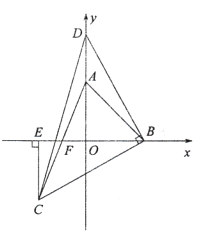
(1)求![]() 的度数;
的度数;
(2)点![]() 是
是![]() 轴正半轴上
轴正半轴上![]() 点上方一点(不与
点上方一点(不与![]() 点重合),以
点重合),以![]() 为腰作等腰
为腰作等腰![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
①求证:![]() ;
;
②连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)45°;(2)①见解析;②(﹣2,0).
【解析】
(1)先根据非负数的性质求得a、b的值,进而可得OA、OB的长,进一步即可求出结果;
(2)①根据余角的性质可得∠ODB=∠CBE,然后即可根据AAS证得结论;
②根据全等三角形的性质和(1)的结论可得BO=CE以及OE的长,然后即可根据AAS证明△AOF≌△CEF,从而可得OF=EF,进而可得结果.
解:(1)∵![]() ,即
,即![]() ,
,
∴a-5=0,b-5=0,∴a=5,b=5,∴AO=BO=5,
∵∠AOB=90°,∴∠ABO=∠BAO=45°;
(2)①证明:∵![]() ,∴∠DBO+∠CBE=90°,
,∴∠DBO+∠CBE=90°,
∵∠ODB+∠DBO=90°,∴∠ODB=∠CBE,
∵∠BOD=∠CEB=90°,BD=CB,
∴![]() (AAS);
(AAS);
②∵![]() ,∴DO=BE,BO=CE,
,∴DO=BE,BO=CE,
∵AO=BO=5,AD=4,∴OE=AD=4,CE=5,
∵∠AOF=∠CEF,∠AFO=∠CFE,AO=CE=5,
∴△AOF≌△CEF(AAS),∴OF=EF,
∵OE=4,∴OF=2,∴点F的坐标是(﹣2,0).


科目:初中数学 来源: 题型:
【题目】我们学过的分解因式的方法有提取公因式法、公式法及十字相乘法,但有很多的多项式只用上述方法就无法分解,如![]() ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为: ![]() ;这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
;这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
(1)分解因式:![]()
(2)![]() 三边
三边![]() ,
,![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 的形状.
的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;(2)求点B到直线OM的距离.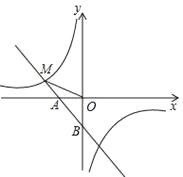
查看答案和解析>>
科目:初中数学 来源: 题型:
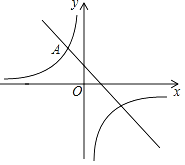
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=﹣x+1的图象的一个交点为A(﹣1,m).
的图象与一次函数y=﹣x+1的图象的一个交点为A(﹣1,m).
(1)求这个反比例函数的表达式;
(2)如果一次函数y=﹣x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y=![]() 的值的范围.
的值的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.
(1)画出直角坐标系xOy,并求出抛物线ADC的函数表达式;
(2)在抛物线型拱壁E、F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人赛跑,两人所跑的路程![]() (米)与所用时间
(米)与所用时间![]() (分)的函数关系如图所示,给出下列结论:①比赛全程1500米;②2分时,甲乙相距300米;③比赛结果是乙比甲领先30秒到达终点;④3分40秒时乙追上甲,其中正确结论的个数为( )
(分)的函数关系如图所示,给出下列结论:①比赛全程1500米;②2分时,甲乙相距300米;③比赛结果是乙比甲领先30秒到达终点;④3分40秒时乙追上甲,其中正确结论的个数为( )
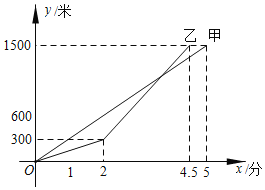
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔![]() 前的平地上选择一点
前的平地上选择一点![]() ,树立测角仪
,树立测角仪![]() ,测出看塔顶的仰角约为
,测出看塔顶的仰角约为![]() ,从
,从![]() 点向塔底
点向塔底![]() 走
走![]() 米到达
米到达![]() 点,测出看塔顶的仰角约为
点,测出看塔顶的仰角约为![]() ,已知测角仪器高为
,已知测角仪器高为![]() 米,则塔
米,则塔![]() 的高大约为
的高大约为![]() ( )
( )
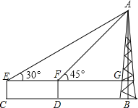
A. 141米 B. 101米 C. 91米 D. 96米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com