
【题目】周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔![]() 前的平地上选择一点
前的平地上选择一点![]() ,树立测角仪
,树立测角仪![]() ,测出看塔顶的仰角约为
,测出看塔顶的仰角约为![]() ,从
,从![]() 点向塔底
点向塔底![]() 走
走![]() 米到达
米到达![]() 点,测出看塔顶的仰角约为
点,测出看塔顶的仰角约为![]() ,已知测角仪器高为
,已知测角仪器高为![]() 米,则塔
米,则塔![]() 的高大约为
的高大约为![]() ( )
( )
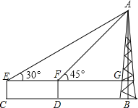
A. 141米 B. 101米 C. 91米 D. 96米
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 两点的坐标分别是点
两点的坐标分别是点![]() ,点
,点![]() ,且
,且![]() 满足:
满足:![]() .
.
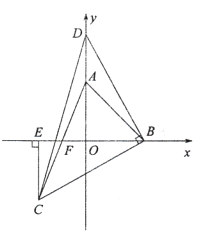
(1)求![]() 的度数;
的度数;
(2)点![]() 是
是![]() 轴正半轴上
轴正半轴上![]() 点上方一点(不与
点上方一点(不与![]() 点重合),以
点重合),以![]() 为腰作等腰
为腰作等腰![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
①求证:![]() ;
;
②连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
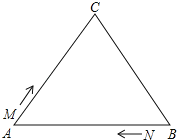
【题目】如图,![]() 中,
中,![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,
分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,![]() 、
、![]() 同时停止运动.
同时停止运动.
(1)点![]() 、
、![]() 运动几秒时,
运动几秒时,![]() 、
、![]() 两点重合?
两点重合?
(2)点![]() 、
、![]() 运动几秒时,可得到等边三角形
运动几秒时,可得到等边三角形![]() ?
?
(3)当点![]() 、
、![]() 在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时
在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时![]() 、
、![]() 运动的时间.
运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
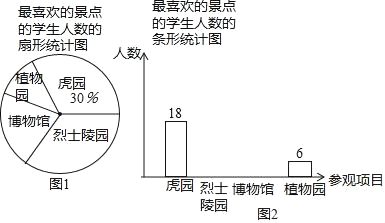
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=32°,则∠OBC的度数为( )
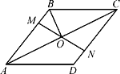
A.32°B.48°C.58°D.68°
查看答案和解析>>
科目:初中数学 来源: 题型:
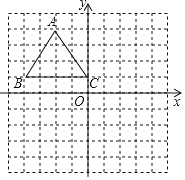
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣2,4),B(﹣4,1),C(0,1).
(1)画出与△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)画出以C1为旋转中心,将△A1B1C1逆时针旋转90°后的△A2B2C2;
(3)尺规作图:连接A1A2,在C1A2边上求作一点P,使得点P到A1A2的距离等于PC1的长(保留作图痕迹,不写作法);
(4)请直接写出∠C1A1P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
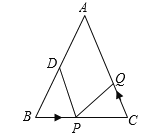
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等, ![]() 与
与![]() 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿![]() 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,
,![]() ,
,![]() .
.

(1)直接写出点![]() 、
、![]() 、
、![]() 关于
关于![]() 轴对称的点
轴对称的点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
![]() ,
, ![]() ,
,![]() ;
;
(2)在图中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() .
.
(3)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com