练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在菱形ABCD中，M、N分别在AB、CD上，且AM＝CN，MN与AC交于点O，连接BO.若∠DAC＝32°，则∠OBC的度数为（ ）

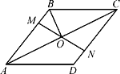
    A.32°B.48°C.58°D.68°

    【答案】C

    【解析】

    根据菱形的性质以及AM=CN，利用ASA可得△AMO≌△CNO，可得AO=CO，然后可得BO⊥AC，继而可求得∠OBC的度数．

    ∵四边形ABCD为菱形，
    ∴AB∥CD，AB=BC，
    ∴∠MAO=∠NCO，∠AMO=∠CNO，
    在△AMO和△CNO中，

    ,

    ∴△AMO≌△CNO（ASA），
    ∴AO=CO，
    ∵AB=BC，
    ∴BO⊥AC，
    ∴∠BOC=90°，
    ∵∠DAC=32°，
    ∴∠BCA=∠DAC=32°，
    ∴∠OBC=90°-32°=58°．
    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】点是双曲线上一点，点是双曲线上一点，轴上有两点，，平行四边形的面积为，则的值是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，某商场有可上行和下行的两条自动扶梯，扶梯上行和下行的长度相等，运行速度相同且保持不变，甲、乙两人同时站上了上行和下行端，甲站上上行扶梯的同时又以0.8米/秒的速度往上走，乙站上下行扶梯后则站立不动随扶梯下行，甲到达扶梯顶端后立即乘坐下行扶梯（换乘时间忽略不计）同时以0.8米/秒的速度往下走，乙到达低端后则在原点等候甲，图②中线段OB、AB分别表示甲、乙两人在乘坐扶梯过程中，高扶梯底端的路程y（米）与所用时间x（秒）的部分函数图象，结合图象解答下列问题：

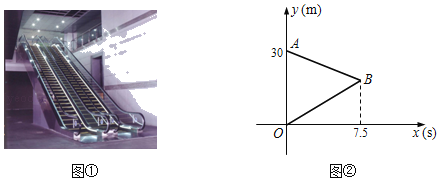
    （1）每条扶梯的长度为　 　米（直接填空）；

    （2）求点B的坐标；

    （3）乙到达扶梯底端后，还需等待　 　秒，甲才到达扶梯底端（直接填空）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

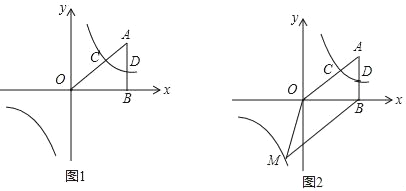
    【题目】如图1，在平面直角坐标系中，A点的坐标为（m，3），AB⊥x轴于点B，tan∠OAB=，反比例函数y1=的图象的一支经过AO的中点C，且与AB交于点D．

    （1）求反比例函数解析式；

    （2）设直线OA的解析式为y2=nx，请直接写出y1＜y2时，自变量x的取值范围　 　．

    （3）如图2，若函数y=3x与y1=的图象的另一支交于点M，求△OMB与四边形OCDB的面积的比值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周末，小明和小华来滨湖新区渡江纪念馆游玩，看到高雄挺拔的“胜利之塔”，萌发了用所学知识测量塔高的想法，如图，他俩在塔前的平地上选择一点，树立测角仪，测出看塔顶的仰角约为，从点向塔底走米到达点，测出看塔顶的仰角约为，已知测角仪器高为米，则塔的高大约为（ ）

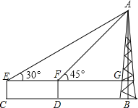
    A. 141米 B. 101米 C. 91米 D. 96米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

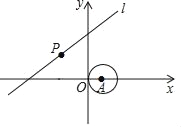
    【题目】如图，在平面直角坐标系中，⊙O的圆心A的坐标为（1，0），半径为1，点P为直线y=x+3上的动点，过点P作⊙A的切线，且点为B，则PB的最小值是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践 美妙的黄金矩形

    阅读理解

    在数学上称短边与长边的比是（约为0.618）的矩形叫做黄金矩形（GoldenRectangle），黄金矩形蕴藏着丰富的美学价值，给我们以协调、匀称的美感．

    （1）某校团委举办“五四手抄报比赛”，手抄报规格统一设计成：长是40cm的黄金矩形，则宽约为__________cm；（精确到0.1cm）

    操作发现 利用一张正方形纸片折叠出一个黄金矩形．

    第一步，如图1，折叠正方形纸片ABCD，使AB和DC重合，得到折痕EF（点E，F分别在边AD，BC上），然后把纸片展平．

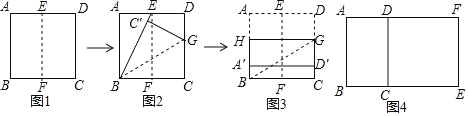
    第二步，如图2，折叠正方形纸片ABCD，使得BC落在BE上，点C′和点C对应，得到折痕BG（点G在CD上），再次纸片展平．

    第三步，如图3，沿过点G的直线折叠正方形纸片ABCD，使点A和点D分别落在AB和CD上，折痕为HG，显然四边形HBCG为矩形．

    （2）在上述操作中，以AB=2为例，证明矩形HBCG是黄金矩形．

    （参考计算： =）

    拓广探索

    （3）“希望小组”的同学通过探究发现：以黄金矩形的长边为一边，在原黄金矩形外作正方形，得到的新矩形仍然是黄金矩形．

    如图4，如果四边形ABCD是黄金矩形（AB＞AD），四边形DCEF是正方形，那么四边形ABEF也是黄金矩形，他们的发现正确吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

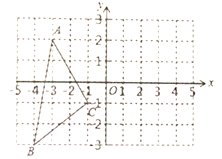
    【题目】如图，（1）在网格中画出关于y轴对称的；

    （2）在y轴上确定一点P，使周长最短，（只需作图，保留作图痕迹）

    （3）写出关于x轴对称的的各顶点坐标；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与直线交于点A，点A的横坐标为，且直线与x轴交于点B，与y轴交于点D，直线与y轴交于点C.

    （1）求点A的坐标及直线的函数表达式；

    （2）连接，求的面积.

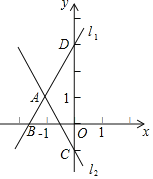
    查看答案和解析>>

    同步练习册答案