
����Ŀ���ۺ���ʵ�� ����Ļƽ����
�Ķ�����
����ѧ�ϳƶ̱��볤�ߵı���![]() ��ԼΪ0.618���ľ��ν����ƽ���Σ�GoldenRectangle�����ƽ�����̲��ŷḻ����ѧ��ֵ����������Э�����ȳƵ����У�
��ԼΪ0.618���ľ��ν����ƽ���Σ�GoldenRectangle�����ƽ�����̲��ŷḻ����ѧ��ֵ����������Э�����ȳƵ����У�
��1��ijУ��ί�ٰ��������ֳ������������ֳ������ͳһ��Ƴɣ�����40cm�Ļƽ���Σ����ԼΪ__________cm������ȷ��0.1cm��
�������� ����һ��������ֽƬ�۵���һ���ƽ���Σ�
��һ������ͼ1���۵�������ֽƬABCD��ʹAB��DC�غϣ��õ��ۺ�EF����E��F�ֱ��ڱ�AD��BC�ϣ���Ȼ���ֽƬչƽ��
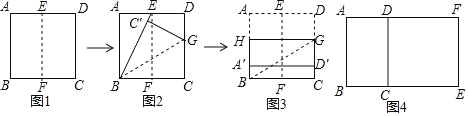
�ڶ�������ͼ2���۵�������ֽƬABCD��ʹ��BC����BE�ϣ���C���͵�C��Ӧ���õ��ۺ�BG����G��CD�ϣ����ٴ�ֽƬչƽ��
����������ͼ3���ع���G��ֱ���۵�������ֽƬABCD��ʹ��A�͵�D�ֱ�����AB��CD�ϣ��ۺ�ΪHG����Ȼ�ı���HBCGΪ���Σ�
��2�������������У���AB=2Ϊ����֤������HBCG�ǻƽ���Σ�
���ο����㣺![]() =
=![]() ��
��
�ع�̽��
��3����ϣ��С������ͬѧͨ��̽�����֣��Իƽ���εij���Ϊһ�ߣ���ԭ�ƽ�������������Σ��õ����¾�����Ȼ�ǻƽ���Σ�
��ͼ4������ı���ABCD�ǻƽ���Σ�AB��AD�����ı���DCEF�������Σ���ô�ı���ABEFҲ�ǻƽ���Σ����ǵķ�����ȷ����˵�����ɣ�
���𰸡���1��24.7����2��֤������������3���ı���ABEF�ǻƽ�������������ȷ.
��������
��1�����ݻƽ���εĶ�����㼴�ɣ�
��2����ͼ2�У�����EG����CG=C��G=x��������![]() ��Rt��EGD��Rt��EGC���У�
��Rt��EGD��Rt��EGC���� ![]() ���
���![]() �ɵ�
�ɵ�![]() ���ɴ˼���֤����
���ɴ˼���֤����
��3����ͼ4�У��ı���ABEF�ǻƽ�������������ȷ����AB=a����AD=BC=![]() a�����AB��BE��ֵ�����жϣ�
a�����AB��BE��ֵ�����жϣ�
�⣺��1����ԼΪ40��![]() ��40��0.681��24.7cm��
��40��0.681��24.7cm��
�ʴ�Ϊ24.7��
��2����ͼ2�У�����EG����CG=C��G=x��
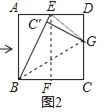
��AB=2��AE=ED=1��
��![]()
��Rt��EGD��Rt��EGC����![]()
���![]()
��![]()
��ͼ3�еľ���HBCG�ǻƽ���Σ�
��3����ͼ4�У��ı���ABEF�ǻƽ�������������ȷ��

���ɣ���AB=a����AD=BC=![]() a��
a��
���ı���DCEF�������Σ�
��DC=DF=EF=CE=a��
��![]()
��![]()
�����ABEF�ǻƽ���Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е������Ǽס��ҡ�������ÿ��ʮ�ε�����Եijɼ������Թ���Ϊ��������10����ÿ����λ1����1�֣�
���������������������˶�Ա�ײ��Գɼ���
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ����֣� | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
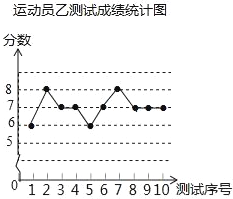
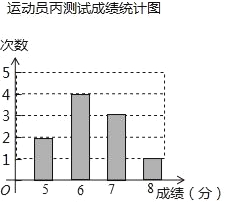
��1��д���˶�Ա�ײ��Գɼ�������Ϊ_____���˶�Ա�Ҳ��Գɼ�����λ��Ϊ_____���˶�Ա�����Գɼ���ƽ����Ϊ_____��
��2�����������˳ɼ��ķ���ֱ�ΪS��2=0.8��S��2=0.4��S��2=0.8�����ۺϷ�����������������ѡ��һλ����ɼ������ҽ�Ϊ�ȶ��Ľ���������Ϊ�����ˣ�����Ϊѡ˭�����ʣ�Ϊʲô��
��3���ס��ҡ��������֮����е�����ϰ��ÿ���˵��ȿ��ܵĴ����������ˣ������ȴӼ����д����������ֽ���ʱ��ص������еĸ����Ƕ��٣�������״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
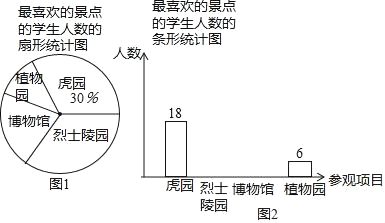
����Ŀ��ijУ��һ�����ʵ����У���֯ѧ���ι��˻�����ʿ��������ݺ�ֲ����Ϊ�˽Ȿ�����ʵ�����Ч����ѧУ�����ȡ�˲���ѧ����������ϲ���ľ������������ʾ����飬������ͳ�ƽ�����������²�������ͳ��ͼ��������ϲ����ʿ����ѧ����������ϲ������ݵ�ѧ������֮��Ϊ2��1������ͳ��ͼ����������⣺
��1�����λ������� ��ѧ����
��2���벹ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У���ϲ��ֲ����ѧ����������Ӧ���ε�Բ�Ľ����� ���ȣ�
��4����У�˴βμ����ʵ�����ѧ����720�ˣ��������ϲ����ʿ��������Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�M��N�ֱ���AB��CD�ϣ���AM��CN��MN��AC���ڵ�O������BO.����DAC��32�������OBC�Ķ���Ϊ�� ��
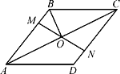
A.32��B.48��C.58��D.68��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
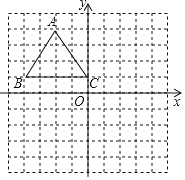
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�������������ֱ�ΪA����2��4����B����4��1����C��0��1����
��1���������ABC����x��ԳƵġ�A1B1C1����д����C1�����ꣻ
��2��������C1Ϊ��ת���ģ�����A1B1C1��ʱ����ת90����ġ�A2B2C2��
��3���߹���ͼ������A1A2����C1A2��������һ��P��ʹ�õ�P��A1A2�ľ������PC1�ij���������ͼ�ۼ�����д��������
��4����ֱ��д����C1A1P�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݡ������ͥ�����Ķ����ѵ��鱨�桷�е���������Ƴ�����ͳ��ͼ����ͼ��֪������˵���������ǣ� ��

A.����ͳ��ͼ�ܷ�ӳ����������������ռ�İٷֱ�
B.ÿ���Ķ�30�������ϵľ����ͥ���ӳ���50%
C.ÿ���Ķ�1Сʱ���ϵľ����ͥ����ռ20%
D.ÿ���Ķ�30������1Сʱ�ľ����ͥ���Ӷ�Ӧ���ε�Բ�Ľ���108��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �У�
�У�![]() ���ף�
���ף�![]() ���ף���
���ף���![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
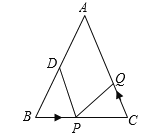
��1�������P���߶�BC����3����/����ٶ���B����C���˶���ͬʱ����Q���߶�CA����C����A���˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���![]() ��
��![]() �Ƿ�ȫ�ȣ���˵�����ɣ�
�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ� ![]() ��
��![]() �Ƿ����ȫ�ȣ����ܣ����ȫ��ʱ��Q���˶��ٶȺ�ʱ�䣻�����ܣ���˵�����ɣ�
�Ƿ����ȫ�ȣ����ܣ����ȫ��ʱ��Q���˶��ٶȺ�ʱ�䣻�����ܣ���˵�����ɣ�
��2������Q�Ԣ��е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ����![]() �����˶������ʱ���P���Q��һ����
�����˶������ʱ���P���Q��һ����![]() ����������������
����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ8cm2 �� AP��ֱ��B��ƽ����BP��P������PBC�����Ϊ�� ��

A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
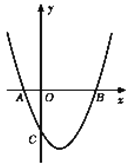
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C��0��
��x�ύ��A��B���㣬��y�ύ�ڵ�C��0��![]() ����
����
��1��![]() _____����A������Ϊ______����B������Ϊ_____��
_____����A������Ϊ______����B������Ϊ_____��
��2����������![]() �Ķ���ΪM�����ı���ABMC�������
�Ķ���ΪM�����ı���ABMC�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com