
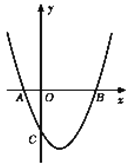
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).
).
(1)![]() _____,点A的坐标为______,点B的坐标为_____;
_____,点A的坐标为______,点B的坐标为_____;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
【答案】(1)-3(-1,0),(3,0)(2)9
【解析】
(1)把点C的坐标代入函数解析式,然后求出k的值即可;令y=0,得到关于x的一元二次方程,解方程求出x的值,再根据点A在点B的左边,写出坐标即可;
(2)把抛物线解析式整理成顶点式,然后写出顶点坐标,再连接OM,分别求出△AOC、△MOC、△MOB的面积,然后根据四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积进行计算即可求解;
(1)∵抛物线y=x22x+k与y轴交于点C(0,3),
∴k=3,
∴抛物线的解析式为y=x22x3,
令y=0,则x22x3=0,
∴(x+1)(x3)=0,
∴x+1=0,x3=0,
解得x1=1,x2=3,
∴点A的坐标为A(1,0),点B的坐标为B(3,0);
故答案为:3,(1,0),(3,0);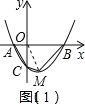
(2)如图(1),∵y=![]() 2x3=
2x3=![]() 4,
4,
∴抛物线的顶点为M(1,4),连接OM,
则△AOC的面积=![]() AOOC=
AOOC=![]() ×1×3=32,△MOC的面积=
×1×3=32,△MOC的面积=![]() OC|xM|=
OC|xM|=![]() ×3×1=
×3×1=![]() ,
,
△MOB的面积=![]() OB|yM|=
OB|yM|=![]() ×3×4=6,
×3×4=6,
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=![]() +
+![]() +6=9.
+6=9.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】综合与实践 美妙的黄金矩形
阅读理解
在数学上称短边与长边的比是![]() (约为0.618)的矩形叫做黄金矩形(GoldenRectangle),黄金矩形蕴藏着丰富的美学价值,给我们以协调、匀称的美感.
(约为0.618)的矩形叫做黄金矩形(GoldenRectangle),黄金矩形蕴藏着丰富的美学价值,给我们以协调、匀称的美感.
(1)某校团委举办“五四手抄报比赛”,手抄报规格统一设计成:长是40cm的黄金矩形,则宽约为__________cm;(精确到0.1cm)
操作发现 利用一张正方形纸片折叠出一个黄金矩形.
第一步,如图1,折叠正方形纸片ABCD,使AB和DC重合,得到折痕EF(点E,F分别在边AD,BC上),然后把纸片展平.
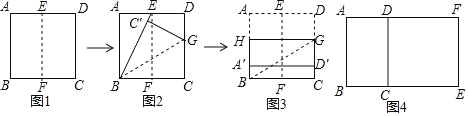
第二步,如图2,折叠正方形纸片ABCD,使得BC落在BE上,点C′和点C对应,得到折痕BG(点G在CD上),再次纸片展平.
第三步,如图3,沿过点G的直线折叠正方形纸片ABCD,使点A和点D分别落在AB和CD上,折痕为HG,显然四边形HBCG为矩形.
(2)在上述操作中,以AB=2为例,证明矩形HBCG是黄金矩形.
(参考计算:![]() =
=![]() )
)
拓广探索
(3)“希望小组”的同学通过探究发现:以黄金矩形的长边为一边,在原黄金矩形外作正方形,得到的新矩形仍然是黄金矩形.
如图4,如果四边形ABCD是黄金矩形(AB>AD),四边形DCEF是正方形,那么四边形ABEF也是黄金矩形,他们的发现正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部门组织调运一批物资,一运送物资车开往距离出发地180千米的目的地,出发第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地.设原计划速度为x千米/小时,则方程可列为( )
A. ![]() +
+![]() =
=![]() B.
B. ![]() -
-![]() =
=![]() C.
C. ![]() +1=
+1=![]() ﹣
﹣![]() D.
D. ![]() +1=
+1=![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 交于点A,点A的横坐标为
交于点A,点A的横坐标为![]() ,且直线
,且直线![]() 与x轴交于点B,与y轴交于点D,直线
与x轴交于点B,与y轴交于点D,直线![]() 与y轴交于点C.
与y轴交于点C.
(1)求点A的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 的面积.
的面积.
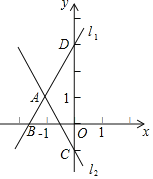
查看答案和解析>>
科目:初中数学 来源: 题型:
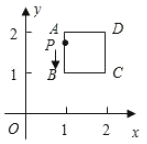
【题目】如图,平面直角坐标系中,在边长为1的正方形![]() 的边上有—动点
的边上有—动点![]() 沿正方形运动一周,
沿正方形运动一周,![]() 则
则![]() 的纵坐标
的纵坐标![]() 与点
与点![]() 走过的路程
走过的路程![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
A. 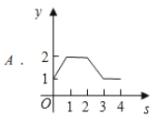 B.
B. 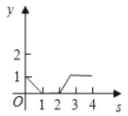 C.
C. 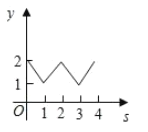 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
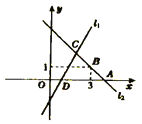
【题目】如图直线![]() 对应的函数表达式为
对应的函数表达式为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)求直线![]() 对应的函数表达式;
对应的函数表达式;
(3)求![]() 的面积;
的面积;
(4)利用函数图象写出关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )

A. 45.2分钟 B. 48分钟 C. 46分钟 D. 33分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线![]() 上,转轴
上,转轴![]() 到地面的距离
到地面的距离![]() ,小亮在荡秋千过程中,当秋千摆动到最高点
,小亮在荡秋千过程中,当秋千摆动到最高点![]() 时,测得点
时,测得点![]() 到
到![]() 的距离
的距离![]() ,点
,点![]() 到地面的距离
到地面的距离![]() :当他从
:当他从![]() 处摆动到
处摆动到![]() 处时,有
处时,有![]() .
.
(1)求![]() 到
到![]() 的距离;
的距离;
(2)求![]() 到地面的距离.
到地面的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、十字相乘法等等,其中十字相乘法在高中应用较多.
十字相乘法:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图),如:将式子![]() 和
和![]() 分解因式,如图:
分解因式,如图:
![]() ;
;
![]() .
.
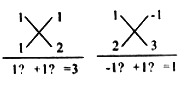
请你仿照以上方法,探索解决下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com