
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() жаЃЌ
жаЃЌ![]() РхУзЃЌ
РхУзЃЌ![]() РхУзЃЌЕу
РхУзЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
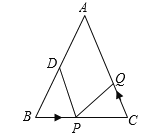
ЃЈ1ЃЉШчЙћЕуPдкЯпЖЮBCЩЯвд3РхУз/УыЕФЫйЖШгЩBЕуЯђCЕудЫЖЏЃЌЭЌЪБЃЌЕуQдкЯпЖЮCAЩЯгЩCЕуЯђAЕудЫЖЏЃЎ
ЂйШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШЯрЕШЃЌОЙ§1УыКѓЃЌ![]() гы
гы![]() ЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЛ
ЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЛ
ЂкШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШВЛЯрЕШЃЌ ![]() гы
гы![]() ЪЧЗёПЩФмШЋЕШЃПШєФмЃЌЧѓГіШЋЕШЪБЕуQЕФдЫЖЏЫйЖШКЭЪБМфЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёПЩФмШЋЕШЃПШєФмЃЌЧѓГіШЋЕШЪБЕуQЕФдЫЖЏЫйЖШКЭЪБМфЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШєЕуQвдЂкжаЕФдЫЖЏЫйЖШДгЕуCГіЗЂЃЌЕуPвддРДЕФдЫЖЏЫйЖШДгЕуBЭЌЪБГіЗЂЃЌЖМФцЪБеыби![]() Ш§БпдЫЖЏЃЌЧѓОЙ§ЖрГЄЪБМфЕуPгыЕуQЕквЛДЮдк
Ш§БпдЫЖЏЃЌЧѓОЙ§ЖрГЄЪБМфЕуPгыЕуQЕквЛДЮдк![]() ЕФФФЬѕБпЩЯЯргіЃП
ЕФФФЬѕБпЩЯЯргіЃП
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌРэгЩМћНтЮіЃЛЂк
ЃЌРэгЩМћНтЮіЃЛЂк![]() УыЃЌ
УыЃЌ![]() РхУз/УыЃЛЃЈ2ЃЉОЙ§
РхУз/УыЃЛЃЈ2ЃЉОЙ§![]() УыЃЌЕу
УыЃЌЕу![]() гыЕу
гыЕу![]() ЕквЛДЮдкБп
ЕквЛДЮдкБп![]() ЩЯЯргі
ЩЯЯргі
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнЁАТЗГЬ=ЫйЖШЁСЪБМфЁБПЩЕУ![]() ЃЌШЛКѓжЄГі
ЃЌШЛКѓжЄГі![]() ЃЌИљОнЕШБпЖдЕШНЧжЄГі
ЃЌИљОнЕШБпЖдЕШНЧжЄГі![]() ЃЌзюКѓРћгУSASМДПЩжЄГіНсТлЃЛ
ЃЌзюКѓРћгУSASМДПЩжЄГіНсТлЃЛ
ЂкИљОнЬтвтПЩЕУ![]() ,Шє
,Шє![]() гы
гы![]() ШЋЕШЃЌдђ
ШЋЕШЃЌдђ![]() ЃЌИљОнЁАТЗГЬЁТЫйЖШ=ЪБМфЁБМЦЫуГіЕуPЕФдЫЖЏЪБМфЃЌМДЮЊЕуQдЫЖЏЕФЪБМфЃЌШЛКѓМДПЩЧѓГіЕуQЕФЫйЖШЃЛ
ЃЌИљОнЁАТЗГЬЁТЫйЖШ=ЪБМфЁБМЦЫуГіЕуPЕФдЫЖЏЪБМфЃЌМДЮЊЕуQдЫЖЏЕФЪБМфЃЌШЛКѓМДПЩЧѓГіЕуQЕФЫйЖШЃЛ
ЃЈ2ЃЉЩшОЙ§![]() УыКѓЕу
УыКѓЕу![]() гыЕу
гыЕу![]() ЕквЛДЮЯргіЃЌИљОнЬтвтПЩЕУЕу
ЕквЛДЮЯргіЃЌИљОнЬтвтПЩЕУЕу![]() гыЕу
гыЕу![]() ЕквЛДЮЯргіЪБЃЌЕуQБШЕуPЖрзпABЃЋAC=20РхУзЃЌСаГіЗНГЬЃЌМДПЩЧѓГіЯргіЪБМфЃЌДгЖјЧѓГіЕуPдЫЖЏЕФТЗГЬЃЌДгЖјХаЖЯГіНсТлЃЎ
ЕквЛДЮЯргіЪБЃЌЕуQБШЕуPЖрзпABЃЋAC=20РхУзЃЌСаГіЗНГЬЃЌМДПЩЧѓГіЯргіЪБМфЃЌДгЖјЧѓГіЕуPдЫЖЏЕФТЗГЬЃЌДгЖјХаЖЯГіНсТлЃЎ
НтЃКЃЈ1ЃЉЂйЁп![]() УыЃЌ
УыЃЌ
Ёр![]() РхУзЃЌ
РхУзЃЌ
Ёп![]() РхУзЃЌЕу
РхУзЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
Ёр![]() РхУзЃЎ
РхУзЃЎ
гжЁп![]() РхУзЃЌ
РхУзЃЌ
Ёр![]() РхУзЃЌ
РхУзЃЌ
Ёр![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
дкЁїBPDКЭЁїCQPжа
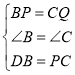
Ёр![]() ЃЎ
ЃЎ
ЂкЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁп![]() гы
гы![]() ШЋЕШЃЌ
ШЋЕШЃЌ
![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЃЌЕу
ЃЌЕу![]() дЫЖЏЕФЪБМф
дЫЖЏЕФЪБМф![]()
![]() УыЃЌ
УыЃЌ
Ёр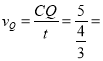
![]() РхУз/УыЃЎ
РхУз/УыЃЎ
ЃЈ2ЃЉЩшОЙ§![]() УыКѓЕу
УыКѓЕу![]() гыЕу
гыЕу![]() ЕквЛДЮЯргіЃЌ
ЕквЛДЮЯргіЃЌ
Ёп![]()
ЁрЕу![]() гыЕу
гыЕу![]() ЕквЛДЮЯргіЪБЃЌЕуQБШЕуPЖрзпABЃЋAC=20РхУз
ЕквЛДЮЯргіЪБЃЌЕуQБШЕуPЖрзпABЃЋAC=20РхУз
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() УыЃЎ
УыЃЎ
ЁрЕу![]() ЙВдЫЖЏСЫ
ЙВдЫЖЏСЫ![]() РхУзЃЎ
РхУзЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁрЕу![]() ЁЂЕу
ЁЂЕу![]() дк
дк![]() БпЩЯЯргіЃЌ
БпЩЯЯргіЃЌ
ЁрОЙ§![]() УыЃЌЕу
УыЃЌЕу![]() гыЕу
гыЕу![]() ЕквЛДЮдкБп
ЕквЛДЮдкБп![]() ЩЯЯргіЃЎ
ЩЯЯргіЃЎ
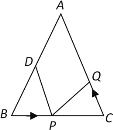


 ЛюСІПЮЪБЭЌВНСЗЯАВсЯЕСаД№АИ
ЛюСІПЮЪБЭЌВНСЗЯАВсЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШбќЁїABCжаЃЌЁЯBAC=90ЁуЃЌBC=4ЃЌPЮЊBCЩЯвЛЖЏЕуЃЌЁЯMPN=45ЁуЃЌPMЁЂPNЗжБ№гыABЁЂACНЛгкЕуEЁЂFЃЌЧвPMЁЭABЃЌBE=x.
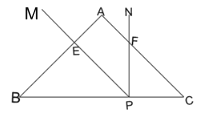
(1)ШєPЕудкBCЩЯдЫЖЏЃЌЧѓЫФБпаЮAEPFЕФУцЛ§ЃЈгУxЕФДњЪ§ЪНБэЪОЃЉВЂаДГіxЕФШЁжЕЗЖЮЇ
(2)ЕБЕуPдкBCЩЯдЫЖЏЪБЃЌЁїEPFФмЗёЮЊжБНЧШ§НЧаЮЃЌШєФмЃЌЧыаДГіДЫЪБxЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈЃКЂйШчЙћСНИіШ§НЧаЮШЋЕШЃЌФЧУДетСНИіШ§НЧаЮвЛЖЈГЩжсЖдГЦЃЛЂкЪ§жсЩЯЕФЕуКЭЪЕЪ§вЛвЛЖдгІЃЛЂлШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂмСНИіЮоРэЪ§ЕФКЭвЛЖЈЮЊЮоРэЪ§ЃЛЂн
ЃЛЂмСНИіЮоРэЪ§ЕФКЭвЛЖЈЮЊЮоРэЪ§ЃЛЂн![]() ОЋШЗЕНЪЎЗжЮЛЃЛЂоШчЙћвЛИіЪ§ЕФЫуЪѕЦНЗНИљЕШгкЫќБОЩэЃЌФЧУДетИіЪ§ЪЧ0.Цфжае§ШЗЕФЫЕЗЈга______.ЃЈЬюађКХЃЉ
ОЋШЗЕНЪЎЗжЮЛЃЛЂоШчЙћвЛИіЪ§ЕФЫуЪѕЦНЗНИљЕШгкЫќБОЩэЃЌФЧУДетИіЪ§ЪЧ0.Цфжае§ШЗЕФЫЕЗЈга______.ЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЕФФкВПЃЌ
ЕФФкВПЃЌ![]() ЃЌдк
ЃЌдк![]() ЁЂ
ЁЂ![]() ЩЯЗжБ№ШЁЕу
ЩЯЗжБ№ШЁЕу![]() ЁЂ
ЁЂ![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжмГЄзюЖЬЃЌдђ
ЕФжмГЄзюЖЬЃЌдђ![]() жмГЄЕФзюаЁжЕЮЊЃЈ ЃЉ
жмГЄЕФзюаЁжЕЮЊЃЈ ЃЉ
A.4B.8C.16D.32
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љx+2гыЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈaЃЌ3ЃЉЃЌBЃЈ3ЃЌbЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈaЃЌ3ЃЉЃЌBЃЈ3ЃЌbЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
(1)ЧѓaЃЌbЕФжЕМАЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
(2)ШєЕуPдкжБЯпy=Љx+2ЩЯЃЌЧвSЁїACP=SЁїBDPЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛ
(3)дкxжсе§АыжсЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУЁїMABЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіMЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌBAЃНBCЃЌDдкБпCBЩЯЃЌЧвDBЃНDAЃНAC
ЃЈ1ЃЉЬюПеЃКШчЭМ1ЃЌЁЯBЃНЁЁ ЁЁЁуЃЌЁЯCЃНЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєMЮЊЯпЖЮBCЩЯЕФЕуЃЌЙ§MзїMHЁЭADЃЌНЛADЕФбгГЄЯпгкЕуHЃЌЗжБ№НЛжБЯпABЁЂACгыЕуNЁЂEЃЎ
ЂйЧѓжЄЃКЁїANEЪЧЕШбќШ§НЧаЮЃЛ
ЂкЯпЖЮBNЁЂCEЁЂCDжЎМфЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
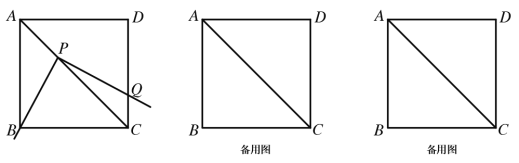
ЁОЬтФПЁПНЋвЛАбШ§НЧГпЗХдкБпГЄЮЊ2ЕФе§ЗНаЮABCDЩЯ(е§ЗНаЮЫФИіФкНЧЮЊ90Ёу,ЫФБпЖМЯрЕШ),ВЂЪЙЫќЕФжБНЧЖЅЕуPдкЖдНЧЯпACЩЯЛЌЖЏ,жБНЧЕФвЛБпЪМжеОЙ§ЕуB,СэвЛБпгыЩфЯпDCНЛгкЕуQЁЃ
ЬНОП:(1)ЕБЕуQдкБпCD ЩЯЪБ,ЯпЖЮPQ гыЯпЖЮPBжЎМфгадѕбљЕФДѓаЁЙиЯЕ?ЪджЄУїФуЙлВьЕУЕННсТлЃЛ
(2)ЕБЕуQдкБпCD ЩЯЪБ,ШчЙћЫФБпаЮ PBCQ ЕФУцЛ§ЮЊ1ЃЌЧѓAPГЄЖШЃЛ
(3)ЕБЕуPдкЯпЖЮAC ЩЯЛЌЖЏЪБ,ЁїPCQ ЪЧЗёПЩФмГЩЮЊЕШбќШ§НЧаЮ?ШчЙћПЩФм,жИГіЫљгаФмЪЙЁїPCQ ГЩЮЊЕШбќШ§НЧаЮЕФЕуQЕФЮЛжУ,ВЂЧѓГіЯргІЕФAPЕФГЄЃЛШчЙћВЛПЩФм,ЪдЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗНГЬЂй![]() ЃЌЂк
ЃЌЂк![]() ЃЌЂл
ЃЌЂл![]() ЃЌЂм
ЃЌЂм![]() ЃЈ
ЃЈ![]() ЮЊЪЕЪ§ЃЉЃЌЂн
ЮЊЪЕЪ§ЃЉЃЌЂн![]() ЃЌЂо
ЃЌЂо![]() ЦфжавЛЖЈЪЧвЛдЊЖўДЮЗНГЬЕФИіЪ§ЮЊЃЈ ЃЉ
ЦфжавЛЖЈЪЧвЛдЊЖўДЮЗНГЬЕФИіЪ§ЮЊЃЈ ЃЉ
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНМвПьЕнЙЋЫОРПМўдБЃЈРПЪеПьМўЕФдБЙЄЃЉЕФШеЙЄзЪЗНАИШчЯТЃК
МзЙЋЫОЮЊЁАЛљБОЙЄзЪ+РПМўЬсГЩЁБЃЌЦфжаЛљБОЙЄзЪЮЊ70дЊ/ШеЃЌУПРПЪевЛМўЬсГЩ2дЊЃЛ
ввЙЋЫОЮоЛљБОЙЄзЪЃЌНівдРПМўЬсГЩМЦЫуЙЄзЪЃЎШєЕБШеРПМўЪ§ВЛГЌЙ§40ЃЌУПМўЬсГЩ4дЊЃЛШєЕБШеНСМўЪ§ГЌЙ§40ЃЌГЌЙ§ВПЗжУПМўЖрЬсГЩ2дЊЃЎ
ШчЭМЪЧНёФъЫФдТЗнМзЙЋЫОРПМўдБШЫОљРПМўЪ§КЭввЙЋЫОНСМўдБШЫОљРПМўЪ§ЕФЬѕаЮЭГМЦЭМЃК

ЃЈ1ЃЉЯжДгНёФъЫФдТЗнЕФ30ЬьжаЫцЛњГщШЁ1ЬьЃЌЧѓетвЛЬьМзЙЋЫОРПМўдБШЫОљРПМўЪ§ГЌЙ§40ЃЈВЛКЌ40ЃЉЕФИХТЪЃЛ
ЃЈ2ЃЉИљОнвдЩЯаХЯЂЃЌвдНёФъЫФдТЗнЕФЪ§ОнЮЊвРОнЃЌВЂНЋИїЙЋЫОРПМўдБЕФШЫОљРПМўЪ§ЪгЮЊИУЙЋЫОИїРПМўдБЕФ
РПМўЪ§ЃЌНтОівдЯТЮЪЬтЃК
ЂйЙРМЦМзЙЋЫОИїРПМўдБЕФШеЦНОљМўЪ§ЃЛ
ЂкаЁУїФтЕНМзЁЂввСНМвЙЋЫОжаЕФвЛМвгІЦИРПМўдБЃЌШчЙћНіДгЙЄзЪЪеШыЕФНЧЖШПМТЧЃЌЧыРћгУЫљбЇЕФЭГМЦжЊЪЖАяЫћбЁдёЃЌОЎЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com