
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љx+2гыЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈaЃЌ3ЃЉЃЌBЃЈ3ЃЌbЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈaЃЌ3ЃЉЃЌBЃЈ3ЃЌbЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
(1)ЧѓaЃЌbЕФжЕМАЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
(2)ШєЕуPдкжБЯпy=Љx+2ЩЯЃЌЧвSЁїACP=SЁїBDPЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛ
(3)дкxжсе§АыжсЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУЁїMABЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіMЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃН![]() ЃЛЃЈ2ЃЉPЃЈ0ЃЌ2ЃЉЛђЃЈЃ3ЃЌ5ЃЉЃЛЃЈ3ЃЉMЃЈ
ЃЛЃЈ2ЃЉPЃЈ0ЃЌ2ЃЉЛђЃЈЃ3ЃЌ5ЃЉЃЛЃЈ3ЃЉMЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЕудкжБЯпЩЯЃЌНЋЕуЕФзјБъДњШыжБЯпНтЮіЪНжаЧѓНтМДПЩЧѓГіaЃЌbЃЌзюКѓгУД§ЖЈЯЕЪ§ЗЈЧѓГіЗДБШР§КЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшГіЕуPзјБъЃЌгУШ§НЧаЮЕФУцЛ§ЙЋЪНЧѓГіSЁїACPЃН![]() ЁС3ЁС|nЃЋ1|ЃЌSЁїBDPЃН
ЁС3ЁС|nЃЋ1|ЃЌSЁїBDPЃН![]() ЁС1ЁС|3n|ЃЌНјЖјНЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЛ
ЁС1ЁС|3n|ЃЌНјЖјНЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЩшГіЕуMзјБъЃЌБэЪОГіMA2ЃНЃЈmЃЋ1ЃЉ2ЃЋ9ЃЌMB2ЃНЃЈm3ЃЉ2ЃЋ1ЃЌAB2ЃН32ЃЌдйШ§жжЧщПіНЈСЂЗНГЬЧѓНтМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпжБЯпyЃНЃxЃЋ2гыЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈaЃЌ3ЃЉЃЌBЃЈ3ЃЌbЃЉСНЕуЃЌЁрЃaЃЋ2ЃН3ЃЌЃ3ЃЋ2ЃНbЃЌ
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈaЃЌ3ЃЉЃЌBЃЈ3ЃЌbЃЉСНЕуЃЌЁрЃaЃЋ2ЃН3ЃЌЃ3ЃЋ2ЃНbЃЌ
ЁрaЃНЃ1ЃЌbЃНЃ1ЃЌ
ЁрAЃЈЃ1ЃЌ3ЃЉЃЌBЃЈ3ЃЌЃ1ЃЉЃЌ
ЁпЕуAЃЈЃ1ЃЌ3ЃЉдкЗДБШР§КЏЪ§yЃН![]() ЩЯЃЌ
ЩЯЃЌ
ЁрkЃНЃ1ЁС3ЃНЃ3ЃЌ
ЁрЗДБШР§КЏЪ§НтЮіЪНЮЊyЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕуPЃЈnЃЌЃnЃЋ2ЃЉЃЌ
ЁпAЃЈЃ1ЃЌ3ЃЉЃЌ
ЁрCЃЈЃ1ЃЌ0ЃЉЃЌ
ЁпBЃЈ3ЃЌЃ1ЃЉЃЌ
ЁрDЃЈ3ЃЌ0ЃЉЃЌ
ЁрSЁїACPЃН![]() ACЁС|xPxA|ЃН
ACЁС|xPxA|ЃН![]() ЁС3ЁС|nЃЋ1|ЃЌSЁїBDPЃН
ЁС3ЁС|nЃЋ1|ЃЌSЁїBDPЃН![]() BDЁС|xBxP|ЃН
BDЁС|xBxP|ЃН![]() ЁС1ЁС|3n|ЃЌ
ЁС1ЁС|3n|ЃЌ
ЁпSЁїACPЃНSЁїBDPЃЌ
Ёр![]() ЁС3ЁС|nЃЋ1|ЃН
ЁС3ЁС|nЃЋ1|ЃН![]() ЁС1ЁС|3n|ЃЌ
ЁС1ЁС|3n|ЃЌ
ЁрnЃН0ЛђnЃН3ЃЌ
ЁрPЃЈ0ЃЌ2ЃЉЛђЃЈ3ЃЌ5ЃЉЃЛ
ЃЈ3ЃЉЩшMЃЈmЃЌ0ЃЉЃЈmЃО0ЃЉЃЌ
ЁпAЃЈ1ЃЌ3ЃЉЃЌBЃЈ3ЃЌ1ЃЉЃЌ
ЁрMA2ЃНЃЈmЃЋ1ЃЉ2ЃЋ9ЃЌMB2ЃНЃЈm3ЃЉ2ЃЋ1ЃЌAB2ЃНЃЈ3ЃЋ1ЃЉ2ЃЋЃЈ13ЃЉ2ЃН32ЃЌ
ЁпЁїMABЪЧЕШбќШ§НЧаЮЃЌ
ЁрЂйЕБMAЃНMBЪБЃЌ
ЁрЃЈmЃЋ1ЃЉ2ЃЋ9ЃНЃЈm3ЃЉ2ЃЋ1ЃЌ
ЁрmЃН0ЃЌЃЈЩсЃЉ
ЂкЕБMAЃНABЪБЃЌ
ЁрЃЈmЃЋ1ЃЉ2ЃЋ9ЃН32ЃЌ
ЁрmЃН1ЃЋ![]() ЛђmЃН1
ЛђmЃН1![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ
ЁрMЃЈ1ЃЋ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
ЂлЕБMBЃНABЪБЃЌЃЈm3ЃЉ2ЃЋ1ЃН32ЃЌ
ЁрmЃН3ЃЋ![]() ЛђmЃН3
ЛђmЃН3![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ
ЁрMЃЈ3ЃЋ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
МДЃКТњзуЬѕМўЕФMЃЈ1ЃЋ![]() ЃЌ0ЃЉЛђЃЈ3ЃЋ
ЃЌ0ЃЉЛђЃЈ3ЃЋ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ


 ЛЅЖЏгЂгяЯЕСаД№АИ
ЛЅЖЏгЂгяЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗДБШР§КЏЪ§![]() ЕФЭМЯёгые§БШР§КЏЪ§
ЕФЭМЯёгые§БШР§КЏЪ§![]() ЕФЭМЯёЖМОЙ§Еу
ЕФЭМЯёЖМОЙ§Еу![]() ЃЌЕу
ЃЌЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯёЩЯЃЌЕу
ЕФЭМЯёЩЯЃЌЕу![]() дке§БШР§КЏЪ§
дке§БШР§КЏЪ§![]() ЕФЭМЯёЩЯ.
ЕФЭМЯёЩЯ.
ЃЈ1ЃЉЧѓДЫе§БШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЯпЖЮABЕФГЄЃЛ
ЃЈ3ЃЉЧѓЁїPABЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЖМЪЧГЃЪ§ЃЌЧв
ЖМЪЧГЃЪ§ЃЌЧв![]() НазіЁАЦцЬиКЏЪ§ЁБЃЌЕБ
НазіЁАЦцЬиКЏЪ§ЁБЃЌЕБ![]() ЪБЃЌЦцЬиКЏЪ§
ЪБЃЌЦцЬиКЏЪ§![]() ОЭГЩЮЊЗДБШР§КЏЪ§
ОЭГЩЮЊЗДБШР§КЏЪ§![]() ЪЧГЃЪ§ЃЌЧв
ЪЧГЃЪ§ЃЌЧв![]() ЃЎ
ЃЎ
![]() ШєОиаЮЕФСНБпГЄЗжБ№ЪЧ
ШєОиаЮЕФСНБпГЄЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() ЃЌЕБСНБпГЄЗжБ№діМг
ЃЌЕБСНБпГЄЗжБ№діМг![]() ЁЂ
ЁЂ![]() КѓЕУЕНЕФаТОиаЮЕФУцЛ§ЪЧ
КѓЕУЕНЕФаТОиаЮЕФУцЛ§ЪЧ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂХаЖЯетИіКЏЪ§ЪЧЗёЁАЦцЬиКЏЪ§ЁБЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂХаЖЯетИіКЏЪ§ЪЧЗёЁАЦцЬиКЏЪ§ЁБЃЛ
![]() ШчЭМдкжБНЧзјБъЯЕжаЃЌЕу
ШчЭМдкжБНЧзјБъЯЕжаЃЌЕу![]() ЮЊдЕуОиаЮ
ЮЊдЕуОиаЮ![]() ЕФЖЅЕуЃЌ
ЕФЖЅЕуЃЌ![]() ЁЂ
ЁЂ![]() зјБъЗжБ№ЮЊ
зјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() жаЕуЃЌСЌНг
жаЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() НЛгк
НЛгк![]() ЃЌЁАЦцЬиКЏЪ§ЁБ
ЃЌЁАЦцЬиКЏЪ§ЁБ![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЁЂ
ЁЂ![]() ЃЌЧѓетИіКЏЪ§ЕФНтЮіЪНЃЌВЂХаЖЯ
ЃЌЧѓетИіКЏЪ§ЕФНтЮіЪНЃЌВЂХаЖЯ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЪЧЗёдкетИіКЏЪ§ЭМЯѓЩЯЃЛ
Ш§ЕуЪЧЗёдкетИіКЏЪ§ЭМЯѓЩЯЃЛ
![]() Ждгк
Ждгк![]() жаЕФЁАЦцЬиКЏЪ§ЁБ
жаЕФЁАЦцЬиКЏЪ§ЁБ![]() ЕФЭМЯѓЃЌФмЗёОЙ§ЪЪЕБЕФБфЛЛКѓгывЛИіЗДБШР§КЏЪ§ЭМЯѓжиКЯЃЌШєФмЃЌЧыжБНгаДГіОпЬхЕФБфЛЛЙ§ГЬКЭетИіЗДБШР§КЏЪ§НтЮіЪНЃЛШєВЛФмЃЌЧыМђЪіРэгЩЃЎ
ЕФЭМЯѓЃЌФмЗёОЙ§ЪЪЕБЕФБфЛЛКѓгывЛИіЗДБШР§КЏЪ§ЭМЯѓжиКЯЃЌШєФмЃЌЧыжБНгаДГіОпЬхЕФБфЛЛЙ§ГЬКЭетИіЗДБШР§КЏЪ§НтЮіЪНЃЛШєВЛФмЃЌЧыМђЪіРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
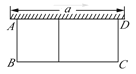
ЁОЬтФПЁПШчЭМЃЌгавЛИіГЄЮЊ24УзЕФРщАЪЃЌвЛУцРћгУЧНЃЈЧНЕФзюДѓГЄЖШaЮЊ15УзЃЉЮЇГЩЕФжаМфИєгавЛЕРРщАЪЕФГЄЗНаЮЛЈЦдЃЎЩшЛЈЦдЕФПэABЮЊxУзЃЌУцЛ§ЮЊSЦНЗНУзЃЎ
ЃЈ1ЃЉЧѓSгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШчЙћвЊЪЙЮЇГЩЛЈЦдУцЛ§зюДѓЃЌЧѓABЕФГЄЮЊЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєСНЬѕХзЮяЯпЕФЖЅЕуЯрЭЌЃЌдђГЦЫќУЧЮЊЁАгбКУХзЮяЯпЁБЃЌХзЮяЯпC1ЃКy1=Љ2x2+4x+2гыC2ЃКu2=Љx2+mx+nЮЊЁАгбКУХзЮяЯпЁБЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпC2ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЕуAЪЧХзЮяЯпC2ЩЯдкЕквЛЯѓЯоЕФЖЏЕуЃЌЙ§AзїAQЁЭxжсЃЌQЮЊДЙзуЃЌЧѓAQ+OQЕФзюДѓжЕЃЎ
ЃЈ3ЃЉЩшХзЮяЯпC2ЕФЖЅЕуЮЊCЃЌЕуBЕФзјБъЮЊЃЈЉ1ЃЌ4ЃЉЃЌЮЪдкC2ЕФЖдГЦжсЩЯЪЧЗёДцдкЕуMЃЌЪЙЯпЖЮMBШЦЕуMФцЪБеыа§зЊ90ЁуЕУЕНЯпЖЮMBЁфЃЌЧвЕуBЁфЧЁКУТфдкХзЮяЯпC2ЩЯЃПШєДцдкЧѓГіЕуMЕФзјБъЃЌВЛДцдкЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() жаЃЌ
жаЃЌ![]() РхУзЃЌ
РхУзЃЌ![]() РхУзЃЌЕу
РхУзЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
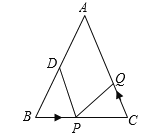
ЃЈ1ЃЉШчЙћЕуPдкЯпЖЮBCЩЯвд3РхУз/УыЕФЫйЖШгЩBЕуЯђCЕудЫЖЏЃЌЭЌЪБЃЌЕуQдкЯпЖЮCAЩЯгЩCЕуЯђAЕудЫЖЏЃЎ
ЂйШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШЯрЕШЃЌОЙ§1УыКѓЃЌ![]() гы
гы![]() ЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЛ
ЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЛ
ЂкШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШВЛЯрЕШЃЌ ![]() гы
гы![]() ЪЧЗёПЩФмШЋЕШЃПШєФмЃЌЧѓГіШЋЕШЪБЕуQЕФдЫЖЏЫйЖШКЭЪБМфЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёПЩФмШЋЕШЃПШєФмЃЌЧѓГіШЋЕШЪБЕуQЕФдЫЖЏЫйЖШКЭЪБМфЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШєЕуQвдЂкжаЕФдЫЖЏЫйЖШДгЕуCГіЗЂЃЌЕуPвддРДЕФдЫЖЏЫйЖШДгЕуBЭЌЪБГіЗЂЃЌЖМФцЪБеыби![]() Ш§БпдЫЖЏЃЌЧѓОЙ§ЖрГЄЪБМфЕуPгыЕуQЕквЛДЮдк
Ш§БпдЫЖЏЃЌЧѓОЙ§ЖрГЄЪБМфЕуPгыЕуQЕквЛДЮдк![]() ЕФФФЬѕБпЩЯЯргіЃП
ЕФФФЬѕБпЩЯЯргіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2ЃЋaxЃЋaЃ2ЃН0.
(1)ЧѓжЄЃКВЛТлaШЁКЮЪЕЪ§ЃЌИУЗНГЬЖМгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
(2)ШєИУЗНГЬЕФвЛИіИљЮЊ1ЃЌЧѓaЕФжЕМАИУЗНГЬЕФСэвЛИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкбЇЯАЭъЕкЪЎЖўеТКѓЃЌеХРЯЪІШУЭЌбЇУЧЖРСЂЭъГЩПЮБО56вГЕк9ЬтЃКЁАШчЭМ1ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЗжБ№ЮЊ
ЃЌДЙзуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.ЁБ
ЕФГЄ.ЁБ

ЃЈ1ЃЉЧыФувВЖРСЂЭъГЩетЕРЬтЃК
ЃЈ2ЃЉД§ЭЌбЇУЧЭъГЩетЕРЬтКѓЃЌеХРЯЪІгжГіЪОСЫвЛЕРЬтЃК
дкПЮБОдЬтЦфЫќЬѕМўВЛБфЕФЧАЬсЯТЃЌНЋ![]() ЫљдкжБЯпа§зЊЕН
ЫљдкжБЯпа§зЊЕН![]() ЕФЭтВПЃЈШчЭМ2ЃЉЃЌЧыФуВТЯы
ЕФЭтВПЃЈШчЭМ2ЃЉЃЌЧыФуВТЯы![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§епжЎМфЕФЪ§СПЙиЯЕЃЌжБНгаДГіНсТлЃК_______.ЃЈВЛашжЄУїЃЉ
Ш§епжЎМфЕФЪ§СПЙиЯЕЃЌжБНгаДГіНсТлЃК_______.ЃЈВЛашжЄУїЃЉ
ЃЈ3ЃЉШчЭМ3ЃЌНЋЃЈ1ЃЉжаЕФЬѕМўИФЮЊЃКдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕудкЭЌвЛЬѕжБЯпЩЯЃЌВЂЧвгаЁЯBEC=ЁЯADC=ЁЯBCA=
Ш§ЕудкЭЌвЛЬѕжБЯпЩЯЃЌВЂЧвгаЁЯBEC=ЁЯADC=ЁЯBCA=![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊШЮвтЖлНЧЃЌФЧУДЃЈ2ЃЉжаФуЕФВТЯыЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃК
ЮЊШЮвтЖлНЧЃЌФЧУДЃЈ2ЃЉжаФуЕФВТЯыЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌA(- 1,5)ЃЌB(- 1,0)ЃЌC(- 4,3)ЃЎ
жаЃЌA(- 1,5)ЃЌB(- 1,0)ЃЌC(- 4,3)ЃЎ

ЃЈ1ЃЉЧѓГіЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉдкЭМжазїГіЁїABCЙигк![]() жсЕФЖдГЦЭМаЮЁїA1B1C1ЃЛ
жсЕФЖдГЦЭМаЮЁїA1B1C1ЃЛ
ЃЈ3ЃЉЩшPЪЧyжсЩЯЕФЕуЃЌвЊЪЙЕУЕуPЕНЕуAЃЌCЕФОрРыКЭзюаЁЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com