
【题目】已知等腰△ABC中,∠BAC=90°,BC=4,P为BC上一动点,∠MPN=45°,PM、PN分别与AB、AC交于点E、F,且PM⊥AB,BE=x.
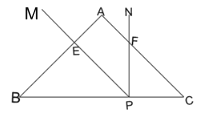
(1)若P点在BC上运动,求四边形AEPF的面积(用x的代数式表示)并写出x的取值范围
(2)当点P在BC上运动时,△EPF能否为直角三角形,若能,请写出此时x的值;若不能,请说明理由.
【答案】(1)四边形AEPF的面积=![]()
![]() ;(2)x的值为
;(2)x的值为![]() 或
或![]() .
.
【解析】
(1)首先证明△ABC、△BEP、△FPC是等腰直角三角形,然后根据等腰直角三角形的边之间的关系求出AB、BP和PC,根据四边形AEPF的面积=![]() 列式整理,然后求出AF,根据AF大于0以及AB=
列式整理,然后求出AF,根据AF大于0以及AB=![]() 可得x的取值范围;
可得x的取值范围;
(2)由∠MPN=45°可知当△EPF为直角三角形时,△EPF是等腰直角三角形,然后分情况讨论:①当∠EFP=90°时,②当∠FEP=90°时,分别根据等腰直角三角形的边之间的关系列出方程求解即可.
解:(1)∵△ABC是等腰直角三角形,且PM⊥AB,
∴△BEP是等腰直角三角形,
∵∠MPN=45°,
∴∠BPN=90°,即PN⊥BC,
∴△FPC是等腰直角三角形,
∵BC=4,BE=x,
∴AB=AC=![]() ,BP=
,BP=![]() ,
,
∴PC=PF=![]() ,
,
∴四边形AEPF的面积=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∵PC=PF=![]() ,
,
∴CF=![]() ,
,
∴AF=AC-CF=![]() ,
,
∵AF>0,即![]() ,
,
∴![]() ,
,
又∵AB=![]() ,
,
∴![]() ,
,
故四边形AEPF的面积=![]()
![]() ;
;
(2)∵∠MPN=45°,
∴当△EPF为直角三角形时,△EPF是等腰直角三角形,
分情况讨论:
①当∠EFP=90°时,EP为斜边,
由(1)可知,EP=x,PF=![]() ,
,
∴EP=![]() PF,即
PF,即![]() ,
,
解得:![]() ;
;
②当∠FEP=90°时,FP为斜边,
由(1)可知,EP=x,PF=![]() ,
,
∴PF=![]() EP,即
EP,即![]() ,
,
解得:![]() ,
,
综上所述,当△EPF为直角三角形时,x的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 CD 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F ,则 BE 的长为_____.
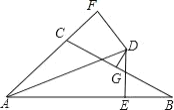
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小明、小红两名同学中选拔一人参加2018年张家界市“经典诗词朗诵”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
小明:80,85,82,85,83 小红:88,79,90,81,72.
回答下列问题:
(1)求小明和小红测试的平均成绩;
(2)求小明和小红五次测试成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与正比例函数
的图像与正比例函数![]() 的图像都经过点
的图像都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 在正比例函数
在正比例函数![]() 的图像上.
的图像上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】"引葭赴岸“是《九章算木》中的- -道題:”今有池一丈 ,葭生其中央,出水一尺,引葭赴岸,迺与岸芥.伺水深,葭氏各几何?"題意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面BC为1尺.如果把该芦苓沿与水池边垂直的方向拉向岸辺,那么芦革的顶部B恰好碰到岸边的B'. 向芦苇长多少? (画出几何图形并解答)
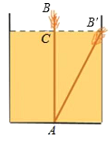
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
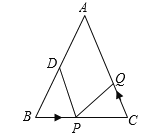
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等, ![]() 与
与![]() 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿![]() 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com