
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
【答案】(1)甲:25万元;乙:28万元;(2)三种方案;甲种套房提升50套,乙种套房提升30套费用最少;(3)当a=3时,三种方案的费用一样,都是2240万元;当a>3时,取m=48时费用最省;当0<a<3时,取m=50时费用最省.
【解析】试题分析:(1)设甲种套房每套提升费用为x万元,根据题意建立方程求出其解即可;
(2)设甲种套房提升m套,那么乙种套房提升(80-m)套,根据条件建立不等式组求出其解就可以求出提升方案,再表示出总费用与m之间的函数关系式,根据一次函数的性质就可以求出结论;
(3)根据(2)表示出W与m之间的关系式,由一次函数的性质分类讨论就可以得出结论.
试题分析:(1)设甲种套房每套提升费用为x万元,依题意,
得![]() 解得:x=25
解得:x=25
经检验:x=25符合题意,x+3=28
答:甲,乙两种套房每套提升费用分别为25万元,28万元.
(2)设甲种套房提升m套,那么乙种套房提升(80-m)套,依题意,得
![]()
解得:48≤m≤50
即m=48或49或50,所以有三种方案分别是:
方案一:甲种套房提升48套,乙种套房提升32套.
方案二:甲种套房提升49套,乙种套房提升31套,
方案三:甲种套房提升50套,乙种套房提升30套.
设提升两种套房所需要的费用为W元.则
W=25m+28×(80-m)=-3m+2240,
∵k=-3<0,
∴W随m的增大而减小,
∴当m=50时,W最少=2090元,即第三种方案费用最少.
(3)在(2)的基础上有:W=(25+a)m+28×(80-m)=(a-3)m+2240
当a=3时,三种方案的费用一样,都是2240万元.
当a>3时,k=a-3>0,
∴W随m的增大而增大,
∴m=48时,费用W最小.
当0<a<3时,k=a-3<0,
∴W随m的增大而减小,
∴m=50时,W最小,费用最省.


科目:初中数学 来源: 题型:
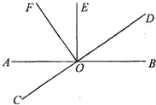
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
(1)图中∠AOF的余角有 ;(把符合条件的角都填出来)
(2)如果∠AOD=140°,那么根据 ,可得∠BOC= 度;
(3)已知5∠EOF=∠AOD,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵大树,它在这个路灯下的影子是MN.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段MQ.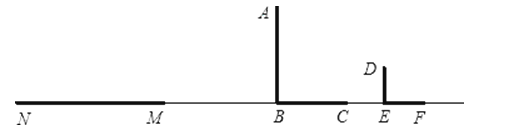
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化解,再求值4![]() -2a-6-2(2a2-2a+3),其中,a=-
-2a-6-2(2a2-2a+3),其中,a=-![]()
(2)已知x=-2,y=3,求![]() x-2(x-
x-2(x-![]() +(-
+(-![]() x+
x+![]() ) 的值,某同学在做此题时,把x=-2 看成了x=2, 但结果也正确,请你帮助分析原因。
) 的值,某同学在做此题时,把x=-2 看成了x=2, 但结果也正确,请你帮助分析原因。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是 ![]() 上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )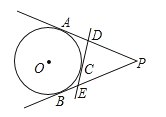
A.12
B.6
C.8
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
A.7
B.8
C.9
D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com