练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，P是⊙O外一点，PA，PB分别和⊙O切于A，B两点，C是 上任意一点，过C作⊙O的切线分别交PA，PB于D，E．若△PDE的周长为12，则PA的长为（　　）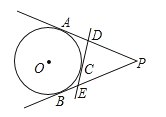

    A.12
    B.6
    C.8
    D.4

    【答案】B
    【解析】解：∵PA，PB分别和⊙O切于A，B两点，
    ∴PA=PB，
    ∵DE是⊙O的切线，
    ∴DA=DC，EB=EC，
    ∵△PDE的周长为12，
    即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12，
    ∴PA=6．
    故选B．
    由PA，PB分别和⊙O切于A，B两点与DE是⊙O的切线，根据切线长定理，即可得PA=PB，DA=DC，EB=EC，又由△PDE的周长为12，易求得PA+PB=12，则可求得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，线段AB＝8cm，C是线段AB上一点，AC＝3.2cm，M是AB的中点，N是AC的中点．

    (1)求线段CM的长；

    (2)求线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高服务质量，某宾馆决定对甲、乙两种套房进行星级提升，已知甲种套房提升费用比乙种套房提升费用少3万元，如果提升相同数量的套房，甲种套房费用为625万元，乙种套房费用为700万元．

    （1）甲、乙两种套房每套提升费用各多少万元？

    （2）如果需要甲、乙两种套房共80套，市政府筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于甲、乙种套房星级提升，市政府对两种套房的提升有几种方案？哪一种方案的提升费用最少？

    （3）在（2）的条件下，根据市场调查，每套乙种套房的提升费用不会改变，每套甲种套房提升费用将会提高a万元（a＞0），市政府如何确定方案才能使费用最少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)观察一列数2，4，8，16，32，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是________；根据此规律，如果an(n为正整数)表示这个数列的第n项，那么a18＝________，an＝________．

    (2)欲求1＋3＋32＋33＋…＋320的值，可令

    S＝1＋3＋32＋33＋…＋320，①

    将①两边同乘3，得__________________，②

    由②减去①，得S＝____________．

    (3)用由特殊到一般的方法知：若数列a1，a2，a3，…，an，从第二项开始每一项与前一项之比的常数为q，则an＝________(用含a1，q，n的代数式表示)．如果这个常数q≠1，求a1＋a2＋a3＋…＋an的值(用含a1，q，n的代数式表示)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列图形都是由同样大小的⊙按一定规律所组成的，其中第1个图形中一共有5个⊙，第2个图形中一共有8个⊙，第3个图形中一共有11个⊙，第4个图形中一共有14个⊙，…，按此规律排列，第1001个图形中基本图形的个数为（　　）

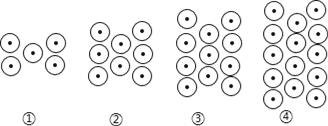
    A. 2998 B. 3001 C. 3002 D. 3005

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E，如果∠BAC=60°，∠ACE=24°，那么∠BCE的大小是（　　）

    A. 24° B. 30° C. 32° D. 36°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB=60°．求：
    （1）PA的长；
    （2）∠COD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以等边三角形ABC的BC边为直径画半圆，分别交AB、AC于点E、D，DF是圆的切线，过点F作BC的垂线交BC于点G．若AF的长为2，则FG的长为（　　）

    A.4
    B.6
    C.3
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分为三个三角形，则S△ABO︰S△BCO︰S△CAO等于（ ）

    A. 1︰1︰1

    B. 1︰2︰3

    C. 2︰3︰4

    D. 3︰4︰5

    查看答案和解析>>

    同步练习册答案