
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
A.4
B.6
C.3![]()
D.2![]()
【答案】B
【解析】解:连接OD,
∵DF为圆O的切线,
∴OD⊥DF,
∵△ABC为等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵OD=OC,
∴△OCD为等边三角形,
∴∠CDO=∠A=60°,∠ABC=∠DOC=60°,
∴OD∥AB,
∴DF⊥AB,
在Rt△AFD中,∠ADF=30°,AF=2,
∴AD=4,即AC=8,
∴FB=AB﹣AF=8﹣2=6,
在Rt△BFG中,∠BFG=30°,
∴BG=3,
则根据勾股定理得:FG=3![]() .
.
故选:B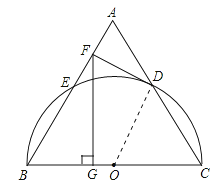
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是 ![]() 上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )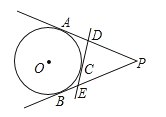
A.12
B.6
C.8
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将坐标为(0,0),(2,1),(2,4),(0,3)的点依次连结起来形成一个图案.
(1)这四个点的横坐标保持不变,纵坐标变成原来的![]() ,将所有的四个点用线段依次连结起来,所得的图案与原图案相比有什么变化?
,将所有的四个点用线段依次连结起来,所得的图案与原图案相比有什么变化?
(2)纵、横坐标分别变成原来的2倍呢?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:
为了保护环境,深圳某公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车每年能节省22.4万汽油,求购买这批混合动力公交车需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为![]() 的中点.
的中点.
(1)求证:AB=BC.
(2)试判断四边形BOCD的形状,并说明理由.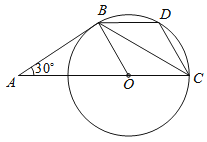
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com