Question

【题目】如图，AB是⊙O的切线，B为切点，圆心O在AC上，∠A=30°，D为的中点．
（1）求证：AB=BC．
（2）试判断四边形BOCD的形状，并说明理由．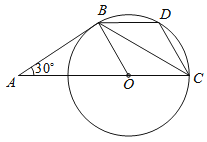

Answer 1

【答案】解：（1）∵AB是⊙O的切线，
∴∠OBA=90°，∠AOB=90°﹣30°=60°．
∵OB=OC，
∴∠OBC=∠OCB，∠OCB=30°=∠A，
∴AB=BC．
（2）四边形BOCD为菱形，
理由如下：连接OD交BC于点M，
∵D是的中点，
∴OD垂直平分BC．
在Rt△OMC中，
∵∠OCM=30°，
∴OC=2OM=OD
∴OM=MD，
∴四边形BOCD为菱形．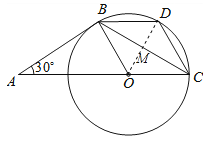

【解析】（1）由AB是⊙O的切线，∠A=30°，易求得∠OCB的度数，继而可得∠A=∠OCB=30°，又由等角对等边，证得AB=BC；
（2）首先连接OD，易证得△BOD与△COD是等边三角形，可得OB=BD=OC=CD，即可证得四边形BOCD是菱形．
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．