
【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
A.7
B.8
C.9
D.10
【答案】C
【解析】解:连结AD,如图,
∵AB为直径,
∴∠ADB=90°,
∴∠1+∠ADE=90°,∠2+∠C=90°,
∵DE为切线,
∴ED=EA,
∴∠ADE=∠2,
∴∠1=∠C,
∴ED=EC,
∴CE=AE,
∵EF∥AB,
∴EF为△ABC的中位线,
∴BF=CF,
而BO=AO,
∴OF为△ABC的中位线,
∴OF∥AE,
∴AE=OF=7.5,
∴AC=2AE=15,
在Rt△ACD中,BC=![]() =
=![]() =25,
=25,
∵∠DCA=∠ACB,
∴△CDA∽△CAB,
∴![]() =
=![]() , 即
, 即![]() =
=![]() ,
,
∴CD=9.
故选C.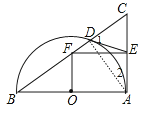
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
A.4
B.6
C.3![]()
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1.将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.如图2.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成2次变换后,骰子朝上一面的点数是________;连续完成2019次变换后,骰子朝上一面的点数是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆轿车在高速公路上匀速行驶.它在经过如下图所示的标志牌下时.速度已达40m/s,并仍以此速度在向前开行.标志牌告诉我们的信息是什么?这辆车是否违反了交通法规?为什么?
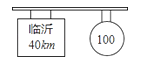
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com