
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
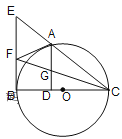
【题目】如图,A是以BC为直径的⊙O上的一点, AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E, 点F是EB的中点,连结CF交AD于点G.
(1)求证:AF是⊙O的切线;
(2)求证:AG=GD;
(3)若FB=FG,且⊙O的半径长为![]() ,求BD.
,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
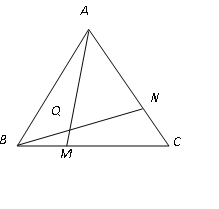
【题目】学完“等腰三角形”一章后,老师布置了一道思考题:如图,点M,N分别在正三角形![]() 的
的![]() 边上,且
边上,且![]() ,
, ![]() 交于点
交于点![]() .求证:
.求证: ![]() .
.
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“![]() ”与“
”与“![]() ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?
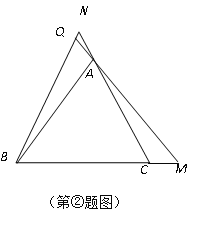
②若将题中的点![]() 分别移动到
分别移动到![]() 的延长线上,是否仍能得到
的延长线上,是否仍能得到![]() ?
?
……
请你作出判断,在下列横线上填写“是”或“否”:① ;② ;选择一个给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问 卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成 了不完整的表格和扇形统计图(如图).
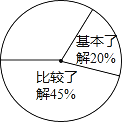
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为 人,表中m的值为 ;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明。(适当添加辅助线,其实并不难)




(1) (2) (3) (4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2﹣8x﹣1=0配方后为( )
A.(x﹣4)2=17
B.(x+4)2=15
C.(x+4)2=17
D.(x﹣4)2=17或(x+4)2=17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家电信公司推出两种移动电话计费方法:计费方法A是每月收月租费58元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过
分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分钟的按每分钟0.20元收通话费.现在设通话时间是
分钟的按每分钟0.20元收通话费.现在设通话时间是![]() 分钟.
分钟.
(1)当通话时间超过![]() 分钟时,请用含
分钟时,请用含![]() 的代数式表示计费方法A的通话费用.
的代数式表示计费方法A的通话费用.
(2)当通话时间超过![]() 分钟时,请用含
分钟时,请用含![]() 的代数式表示计费方法B的通话费用.
的代数式表示计费方法B的通话费用.
(3)用计费方法A的用户一个月累计通话360分钟所需的话费,若改用计费方法B,则可通话多少分钟?
(4)请你分析,当通话时间超过多少分钟时采用计费方法B合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com