
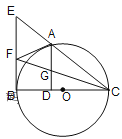
【题目】如图,A是以BC为直径的⊙O上的一点, AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E, 点F是EB的中点,连结CF交AD于点G.
(1)求证:AF是⊙O的切线;
(2)求证:AG=GD;
(3)若FB=FG,且⊙O的半径长为![]() ,求BD.
,求BD.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
试题分析:(1)连接AB, OA,根据直径所对的圆周角是直角可得∠BAC=90°,∠BAE=90°,根据切线的判定与性质可证明;
(2)利用相似三角形的性质与判定可证明;
(3)过点F作FH⊥AD于点H,由等腰三角形和相似三角形的性质与判定可求解.
试题解析:(1)连接AB, OA,
∵BC是直径
∴∠BAC=90°,∠BAE=90°
∵点F是EB的中点
∴AF=BF=EF
∵AF=BF
∴∠FBA=∠FAB
∵OB=OA
∴∠OBA=∠OAB
∴∠FBD=∠FAO
∵BF是⊙O的切线
∴∠FBD=90°
∴∠FAO=90°
∴AF是⊙O的切线。
(2)∵AD⊥BC,∠FBD=90°
∴EB∥AD
∴△FBC∽△GDC, △EBC∽△ADC
∴![]() ,
,![]()
∴![]()
∵EF=FB
∴AG=GD
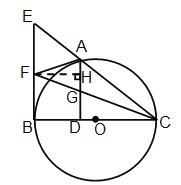
(3)过点F作FH⊥AD于点H
∵AD⊥BC, FH⊥AD
∴FH∥BC
∴∠FHG=∠GDO, ∠HFG=∠DCG
∴△HFG∽△DCG
∵AD⊥BC, FH⊥AD,EB⊥BC
∴四边形HFBD是矩形
∴FH=BD
∵FG=FB,FB=FA
∴FA=FG
∴△AFG是等腰三角形
∴![]() ,
,
∵AG=GD
∴![]()
设BD=x,则FH=x,CD=![]()
∵△HFG∽△DCG
∴![]()
∴![]()
![]()
∴BD=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】上海世博会的某纪念品原价168元,连续两次降价a%后售价为128元.下列所列方程中正确的是( )
A.168(1+a)2=128
B.168(1﹣a%)2=128
C.168(1﹣2a%)=128
D.168(1﹣a2%)=128
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对二次函数y=3(x﹣6)2+9的说法正确的是( )
A. 开口向下 B. 最大值为9
C. 对称轴为直线x=6 D. x<6时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度.其行走路线如图所示.
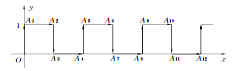
(1)填写下列各点的坐标:
A1 ,A3 ,A12 ;
(2)指出蚂蚁从点A100到A101的移动方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )
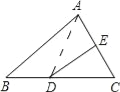
A. 22cm B. 20cm C. 18cm D. 15cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.

(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com