练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）先化解，再求值4-2a-6-2(2a2-2a+3),其中，a=-

    （2）已知x=-2,y=3,求x-2(x-+(-x+) 的值，某同学在做此题时，把x=-2 看成了x=2, 但结果也正确，请你帮助分析原因。

    【答案】(1). 2a-12,-13; (2).原因见解析，y2.

    【解析】

    （1）先去括号合并同类项化简，再把代入计算即可；

    （2）把所给代数式去括号合并同类项化简后即可看出原因.

    解(1)：原式= 4a2-2a-6-4a2+4a-6=2a-12.当a=-时，2a-12=2×（-）-12=-13

    (2)原因:因为化简后没有了含x的项，与x 的值无关.(表述清楚即可)

    原式= x-2x+x2-x+y2=(-2-)x+(+)y2=0+y2=y2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，△AOB为等腰直角三角形，A（4，4）

    （1）求B点坐标；

    （2）如图2，若C为x正半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=90°，连接OD，求∠AOD的度数；

    （3）如图3，过点A作y轴的垂线交y轴于E，F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH，过A作x轴垂线交EH于点M，连FM，等式AM=FM+OF是否成立？若成立，请说明；若不成立，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

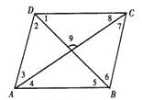
    【题目】如图，∠3和∠9是直线________、_______被直线_______所截而成的______角；∠6和∠9是直线_____、______被直线________所截而成的_______角.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知Rt△ABC中，∠C=90°，AC=6，BC=8，点O和M分别为Rt△ABC的外心和内心，线段OM的长为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高服务质量，某宾馆决定对甲、乙两种套房进行星级提升，已知甲种套房提升费用比乙种套房提升费用少3万元，如果提升相同数量的套房，甲种套房费用为625万元，乙种套房费用为700万元．

    （1）甲、乙两种套房每套提升费用各多少万元？

    （2）如果需要甲、乙两种套房共80套，市政府筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于甲、乙种套房星级提升，市政府对两种套房的提升有几种方案？哪一种方案的提升费用最少？

    （3）在（2）的条件下，根据市场调查，每套乙种套房的提升费用不会改变，每套甲种套房提升费用将会提高a万元（a＞0），市政府如何确定方案才能使费用最少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点N为△ABC的内心，延长AN交BC于点D，交△ABC的外接圆于点E．
    （1）求证：EB=EN=EC；
    （2）求证：NE2=AEDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)观察一列数2，4，8，16，32，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是________；根据此规律，如果an(n为正整数)表示这个数列的第n项，那么a18＝________，an＝________．

    (2)欲求1＋3＋32＋33＋…＋320的值，可令

    S＝1＋3＋32＋33＋…＋320，①

    将①两边同乘3，得__________________，②

    由②减去①，得S＝____________．

    (3)用由特殊到一般的方法知：若数列a1，a2，a3，…，an，从第二项开始每一项与前一项之比的常数为q，则an＝________(用含a1，q，n的代数式表示)．如果这个常数q≠1，求a1＋a2＋a3＋…＋an的值(用含a1，q，n的代数式表示)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E，如果∠BAC=60°，∠ACE=24°，那么∠BCE的大小是（　　）

    A. 24° B. 30° C. 32° D. 36°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1．将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．如图2.若骰子的初始位置为图1所示的状态，那么按上述规则连续完成2次变换后，骰子朝上一面的点数是________；连续完成2019次变换后，骰子朝上一面的点数是________．

    查看答案和解析>>

    同步练习册答案