Question

如图，AB是半圆O的直径，AB=2，射线AM、BM为半圆O的切线，在AM上取一点D，连接BD交半圆于点C，连接AC，过O点作OE⊥BC，延长OE交BN于点F，过D点作半圆O的切线DP，并延长交BN于点Q。
（1）求证：△ACB∽△OBF；
（2）当△ABD与△BFO的面积相等时，求BQ的长；
（3）求证：当D在AM上移动时（A点除外），点Q始终是线段BF的中点。

Answer 1

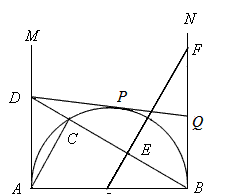
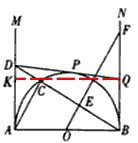
解：（1）∵AB为直径， ∴∠ACB=90°， 即：AC⊥BC， 又∵OE⊥BC， ∴OE∥AC， ∴∠BAC=∠FOB， 又∵BN是半圆的切线， ∴∠BCA=∠FBO=90°， ∴△ACB∽△OBF；
（2）由△ACB∽△OBF得，∠OFB=∠DBA，∠DAB=∠OBF=90°， ∴△ABD∽△BFO， △ABD与△BFO的面积相等时，△ABD≌△BFO， ∴AD=OB=1， 如图，连接OP， ∵DPQ是半圆O的切线， ∴AO=OP=DP=AD=1，OP⊥DP， ∴四边形AOPD是正方形， ∴四边形OBQP是正方形， ∴BQ=OB=1；
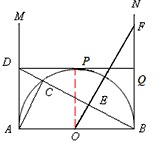（3）由（2）知，△ABD∽△BFO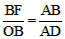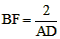， ∴， ∴， ∵DPQ是半圆O的切线， ∴AD=DP，QB=BQ， 过Q点作AM的垂线QK，垂足为K， 在Rt△DQK中， DQ2=QK2+DK2， ∴（AD+BQ）2=22+（AD-BQ）2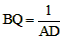， ∴， ∴BF=2BQ， ∴Q为BF的中点。