
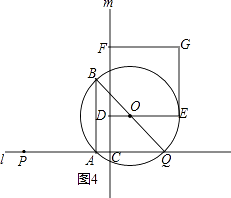
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.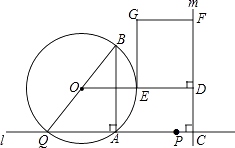
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
【答案】
(1)解:在Rt△ABQ中,
∵AQ:AB=3:4,AQ=3x,
∴AB=4x,
∴BQ=5x,
∵OD⊥m,m⊥l,
∴OD∥l,
∵OB=OQ,
∴ ![]() =2x,
=2x,
∴CD=2x,
∴FD= ![]() =3x
=3x
(2)解:∵AP=AQ=3x,PC=4,
∴CQ=6x+4,
作OM⊥AQ于点M(如图1),
∴OM∥AB,
∵⊙O是△ABQ的外接圆,∠BAQ=90°,
∴点O是BQ的中点,
∴QM=AM= ![]() x
x
∴OD=MC= ![]() ,
,
∴OE= ![]() BQ=
BQ= ![]() ,
,
∴ED=2x+4,
S矩形DEGF=DFDE=3x(2x+4)=90,
解得:x1=﹣5(舍去),x2=3,
∴AP=3x=9
(3)解:①若矩形DEGF是正方形,则ED=DF,
I.点P在A点的右侧时(如图1)
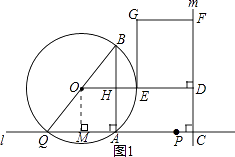
∴2x+4=3x,解得:x=4,
∴AP=3x=12;
II.点P在A点的左侧时,
当点C在Q右侧,
0<x< ![]() 时(如图2),
时(如图2),
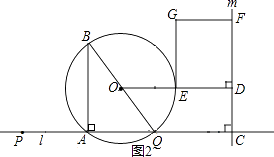
∵ED=4﹣7x,DF=3x,
∴4﹣7x=3x,解得:x= ![]() ,
,
∴AP= ![]() ;
;
当 ![]() ≤x<
≤x< ![]() 时(如图3),
时(如图3),
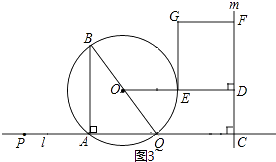
∵ED=4﹣7x,DF=3x,
∴4﹣7x=3x,解得:x= ![]() (舍去),
(舍去),
当点C在Q的左侧时,即x≥ ![]() (如图4),
(如图4),
DE=7x﹣4,DF=3x,
∴7x﹣4=3x,解得:x=1,
∴AP=3,
综上所述:当AP为12或 ![]() 或3时,矩形DEGF是正方形;
或3时,矩形DEGF是正方形;
②连接NQ,由点O到BN的弦心距为l,得NQ=2,
当点N在AB的左侧时(如图5),
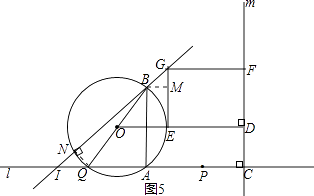
过点B作BM⊥EG于点M,
∵GM=x,BM=x,
∴∠GBM=45°,
∴BM∥AQ,
∴AI=AB=4x,
∴IQ=x,
∴NQ= ![]() =2,
=2,
∴x=2 ![]() ,
,
∴AP=6 ![]() ;
;
当点N在AB的右侧时(如图6),
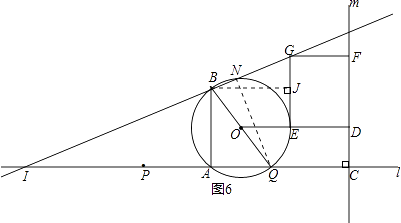
过点B作BJ⊥GE于点J,
∵GJ=x,BJ=4x,
∴tan∠GBJ= ![]() ,
,
∴AI=16x,
∴QI=19x,
∴NQ= ![]() =2,
=2,
∴x= ![]() ,
,
∴AP= ![]() ,
,
综上所述:AP的长为6 ![]() 或
或 ![]() .
.
【解析】(1)设出参数x,由垂径定理可得平分,线段互相代换得出结果;(2)点P的整个运动过程中分为几个过程,须分类 讨论:P在A点的右侧;点P在A点的左侧时;点C在Q的左侧时;可假设矩形DEGF是正方形, 由正方形的性质四条边相等, 得出AP的长; 若BN的弦心距为1,它是![]() BNQ的中位线,得出NQ=2,分类 讨论:N在AB的左侧时;点N在AB的右侧时;利用平行相似性或三角函数,可求出AP.
BNQ的中位线,得出NQ=2,分类 讨论:N在AB的左侧时;点N在AB的右侧时;利用平行相似性或三角函数,可求出AP.


科目:初中数学 来源: 题型:
【题目】如图①,点P是正方形ABCD的BC边上的一点,以DP为边长的正方形DEFP与正方形ABCD在BC的同侧,连接AC,FB.
(1)请你判断FB与AC又怎样的位置关系?并证明你的结论;
(2)若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由;
(3)当点P在射线CB上运动时,请你指出点E的运动路线,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在网格点上,建立如图所示的平面直角坐标系.
(1)请根据如图所示的平面直角坐标系,写出△ABC各点的坐标,并求出△ABC的面积.
(2)把△ABC平移到△A1B1C1,使点B1与原点O重合,按要求画出△A1B1C1,并写出平移过程.
(3)已知P是△ABC内有一点,平移至△A1B1C1后,P点对应点的坐标为P1 (a,b),试写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() 于
于![]() ,
,![]() 交于点
交于点![]() .
.
(1)如图1,请写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)如图2,若![]() 平分
平分![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,连接![]() ,若
,若![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x+k和双曲线y= ![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.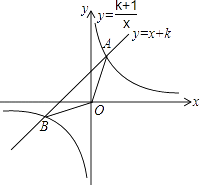
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1 , 当k=2时,△OAB的面积记为S2 , …,依此类推,当k=n时,△OAB的面积记为Sn , 若S1+S2+…+Sn= ![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2015,则m的值是( )
A.43B.44C.45D.46
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com