
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() 于
于![]() ,
,![]() 交于点
交于点![]() .
.
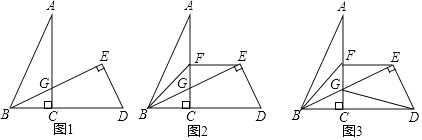
(1)如图1,请写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)如图2,若![]() 平分
平分![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,连接![]() ,若
,若![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1) ![]() ;(2) 见解析;(3)
;(2) 见解析;(3) ![]() .
.
【解析】
(1)根据三角形的内角和定理可得∠DBE=180°-∠E-∠BDE=90°-∠BDE,∠A=180°-∠ACB-∠ABC=90°-∠ABC,再结合已知条件即可证出结论;
(2)根据角平分线的定义和三角形的内角和定理证出∠A=∠FEB,再结合(1)的结论可证∠FEB=∠DBE,根据平行线的判定证出EF∥BD,从而证出∠EFC=∠ACB=90°,再根据垂直的定义即可证出结论;
(3)连接AD、DF,根据三角形中线的性质可知S△ABF=S△BCF=2S△BCG,结合已知条件即可求出S△BCG=![]() ,再根据等高时,面积比等于底之比即可求出S△BDG=8,再根据三角形的面积公式即可求出结论.
,再根据等高时,面积比等于底之比即可求出S△BDG=8,再根据三角形的面积公式即可求出结论.
解:(1)∠A=∠DBE,理由如下
∵![]()
∴∠E=90°
∴∠DBE=180°-∠E-∠BDE=90°-∠BDE
∵![]()
∴∠A=180°-∠ACB-∠ABC=90°-∠ABC
∵![]()
∴∠A=∠DBE
(2)∵![]() 平分
平分![]() ,
,
∴∠ABF=∠EBF
∵![]()
∴∠A=180°-∠ABF-∠AFB=180°-∠EBF-∠EFB=∠FEB
由(1)知∠A=∠DBE
∴∠FEB=∠DBE
∴EF∥BD
∴∠EFC=∠ACB=90°,
∴![]() ;
;
(3)连接AD、DF
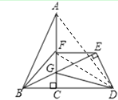
∵![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,
∴S△ABF=S△BCF=2S△BCG
∵![]()
∴S△ADF=![]() S△ABF=3S△BCG,BC:CD=
S△ABF=3S△BCG,BC:CD=![]() =2:3
=2:3
∴BC:BD=2:5
∵![]()
∴![]()
∴S△BCG=![]()
∵S△BCG:S△BDG=BC:BD
即![]() :S△BDG=2:5
:S△BDG=2:5
解得S△BDG=8
∴![]() BG·DE=8
BG·DE=8
∵![]()
∴![]() BG2=8
BG2=8
解得BG=4或-4(不符合实际,舍去)
即BG=4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图 1,直线![]() 分别交
分别交![]() 于点
于点![]() (点
(点![]() 在点
在点![]() 的右侧),若
的右侧),若![]()
(1)求证:![]() ;
;

(2)如图2所示,点![]() 在
在![]() 之间,且位于
之间,且位于![]() 的异侧,连
的异侧,连![]() , 若
, 若![]() ,则
,则![]() 三个角之间存在何种数量关系,并说明理由.
三个角之间存在何种数量关系,并说明理由.

(3)如图 3 所示,点![]() 在线段
在线段![]() 上,点
上,点![]() 在直线
在直线![]() 的下方,点
的下方,点![]() 是直线
是直线![]() 上一点(在
上一点(在![]() 的左侧),连接
的左侧),连接![]() ,若
,若![]() ,则请直接写出
,则请直接写出![]() 与
与![]() 之间的数量
之间的数量

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.

(1)求证:△OAE≌△OCF;
(2)若OA=OD,猜想:四边形ABCD的形状,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(6,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售![]() 、
、![]() 两种型号的新能源汽车,上周售出1辆
两种型号的新能源汽车,上周售出1辆![]() 型车和3辆
型车和3辆![]() 型车,销售额为96万元:本周售出2辆
型车,销售额为96万元:本周售出2辆![]() 型车和1辆
型车和1辆![]() 型车,销售额为62万元.
型车,销售额为62万元.
(1)求每辆车![]() 型车和
型车和![]() 型车的售价各多少万元?
型车的售价各多少万元?
(2)甲公司拟向该商店购买![]() 、
、![]() 两种型号的新能源汽车共6辆,购车总费用不超过140万元,则至少购进
两种型号的新能源汽车共6辆,购车总费用不超过140万元,则至少购进![]() 型车多少辆?
型车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.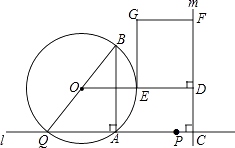
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 、
、![]() 的交点为
的交点为![]() ,现作如下操作:
,现作如下操作:
第一次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第二次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第三次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
…
第![]() 次操作,分别作
次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() .
.
若![]() 度,那
度,那![]() 等于__________度.
等于__________度.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com