
【题目】如图 1,直线![]() 分别交
分别交![]() 于点
于点![]() (点
(点![]() 在点
在点![]() 的右侧),若
的右侧),若![]()
(1)求证:![]() ;
;

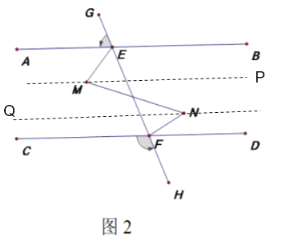
(2)如图2所示,点![]() 在
在![]() 之间,且位于
之间,且位于![]() 的异侧,连
的异侧,连![]() , 若
, 若![]() ,则
,则![]() 三个角之间存在何种数量关系,并说明理由.
三个角之间存在何种数量关系,并说明理由.

(3)如图 3 所示,点![]() 在线段
在线段![]() 上,点
上,点![]() 在直线
在直线![]() 的下方,点
的下方,点![]() 是直线
是直线![]() 上一点(在
上一点(在![]() 的左侧),连接
的左侧),连接![]() ,若
,若![]() ,则请直接写出
,则请直接写出![]() 与
与![]() 之间的数量
之间的数量

【答案】(1)证明过程见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ∠N+∠PMH=180°.
∠N+∠PMH=180°.
【解析】
(1)根据同旁内角互补,两直线平行即可判定AB∥CD;
(2)设∠N=![]() ,∠M=
,∠M=![]() ,∠AEM=
,∠AEM=![]() ,∠NFD=
,∠NFD=![]() ,过M作MP∥AB,过N作NQ∥AB可得∠PMN=
,过M作MP∥AB,过N作NQ∥AB可得∠PMN=![]() -
-![]() ,∠QNM=
,∠QNM=![]() -
-![]() ,根据平行线性质得到
,根据平行线性质得到![]() -
-![]() =
=![]() -
-![]() ,化简即可得到
,化简即可得到![]() ;
;
(3)过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R,根据平行线的性质可得∠BPM=∠PMI,由已知得到∠MON=∠MPN+∠PMI=3∠PMI及∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD,根据对顶角相等得到∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM,化简得到∠FNP+2∠PMI-2∠RFM=180°-∠PMH,根据平行线的性质得到3∠PMI+∠FNP+∠FNH=180°及3∠RFM+∠FNH=180°,两个等式相减即可得到∠RFM-∠PMI=![]() ∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到
∠FNP,将该等式代入∠FNP+2∠PMI-2∠RFM=180°-∠PMH,即得到![]() ∠FNP=180°-∠PMH,即
∠FNP=180°-∠PMH,即![]() ∠N+∠PMH=180°.
∠N+∠PMH=180°.
(1)证明:∵∠1=∠BEF,![]()
∴∠BEF+∠2=180°
∴AB∥CD.
(2)解:![]()
设∠N=![]() ,∠M=
,∠M=![]() ,∠AEM=
,∠AEM=![]() ,∠NFD=
,∠NFD=![]()
过M作MP∥AB,过N作NQ∥AB
∵![]() ,MP∥AB,NQ∥AB
,MP∥AB,NQ∥AB
∴MP∥NQ∥AB∥CD
∴∠EMP=![]() ,∠FNQ=
,∠FNQ=![]()
∴∠PMN=![]() -
-![]() ,∠QNM=
,∠QNM=![]() -
-![]()
∴![]() -
-![]() =
=![]() -
-![]()
即![]() =
=![]() -
-![]()
∴![]()
故答案为![]()
(3)解:![]() ∠N+∠PMH=180°
∠N+∠PMH=180°
过点M作MI∥AB交PN于O,过点N作NQ∥CD交PN于R.
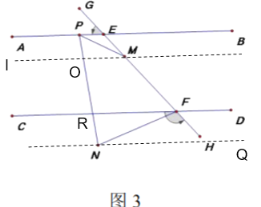
∵![]() ,MI∥AB,NQ∥CD
,MI∥AB,NQ∥CD
∴AB∥MI∥NQ∥CD
∴∠BPM=∠PMI
∵∠MPN=2∠MPB
∴∠MPN=2∠PMI
∴∠MON=∠MPN+∠PMI=3∠PMI
∵∠NFH=2∠HFD
∴∠RFN=180°-∠NFH-∠HFD=180°-3∠HFD
∵∠RFN=∠HFD
∴∠PRF=∠FNP+∠RFN=∠FNP+180°-3∠RFM
∴∠MON+∠PRF+∠RFM=360°-∠OMF
即3∠PMI+∠FNP+180°-3∠RFM+∠RFM=360°-∠OMF
∴∠FNP+2∠PMI-2∠RFM=180°-∠PMH
∵3∠PMI+∠PNH=180°
∴3∠PMI+∠FNP+∠FNH=180°
∵3∠RFM+∠FNH=180°
∴3∠PMI-3∠RFM+∠FNP=0°
即∠RFM-∠PMI=![]() ∠FNP
∠FNP
∴∠FNP+2∠PMI-2∠RFM=∠FNP-2(∠RFM-∠PMI)=180°-∠PMH
∠FNP-2×![]() ∠FNP=180°-∠PMH
∠FNP=180°-∠PMH
![]() ∠FNP=180°-∠PMH
∠FNP=180°-∠PMH
即![]() ∠N+∠PMH=180°
∠N+∠PMH=180°
故答案为![]() ∠N+∠PMH=180°
∠N+∠PMH=180°


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在面积为3的正方形ABCD中,E,F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b,已知T(1,1)=2.5,T(4,﹣2)=4.
=b,已知T(1,1)=2.5,T(4,﹣2)=4.
(1)求a,b的值;
(2)若关于m的不等式组![]() 恰好有2个整数解,求实数P的取值范围.
恰好有2个整数解,求实数P的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点P是正方形ABCD的BC边上的一点,以DP为边长的正方形DEFP与正方形ABCD在BC的同侧,连接AC,FB.
(1)请你判断FB与AC又怎样的位置关系?并证明你的结论;
(2)若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由;
(3)当点P在射线CB上运动时,请你指出点E的运动路线,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )

A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() 于
于![]() ,
,![]() 交于点
交于点![]() .
.
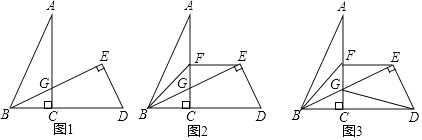
(1)如图1,请写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)如图2,若![]() 平分
平分![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,连接![]() ,若
,若![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com