
【题目】如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在梯形内画出一个最大的扇形,则阴影部分的面积为 . 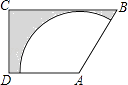
【答案】10 ![]() ﹣4π
﹣4π
【解析】解:如图设扇形与BC相切于点E,连接AE,则AE⊥BC.
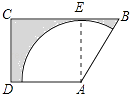
∵AD∥BC,∠C=90°,
∴∠D=∠C=∠AEC=90°,
∴四边形ADCE是矩形,
∴AD=CE=4,
∵BC=6,
∴BE=2,
在RT△AEB中,∵∠AEB=90°,AB=4,EB=2,
∴AE= ![]() =2
=2 ![]() ,AB=2EB,
,AB=2EB,
∴∠EAB=30°,
∵∠DAE=90°,
∴∠DAB=120°,
∴S阴=S梯形ABCD﹣ ![]() =
= ![]() (4+6)
(4+6) ![]() ﹣
﹣ ![]() =10
=10 ![]() ﹣4π.
﹣4π.
所以答案是10 ![]() ﹣4π
﹣4π
【考点精析】根据题目的已知条件,利用扇形面积计算公式的相关知识可以得到问题的答案,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售![]() 、
、![]() 两种型号的新能源汽车,上周售出1辆
两种型号的新能源汽车,上周售出1辆![]() 型车和3辆
型车和3辆![]() 型车,销售额为96万元:本周售出2辆
型车,销售额为96万元:本周售出2辆![]() 型车和1辆
型车和1辆![]() 型车,销售额为62万元.
型车,销售额为62万元.
(1)求每辆车![]() 型车和
型车和![]() 型车的售价各多少万元?
型车的售价各多少万元?
(2)甲公司拟向该商店购买![]() 、
、![]() 两种型号的新能源汽车共6辆,购车总费用不超过140万元,则至少购进
两种型号的新能源汽车共6辆,购车总费用不超过140万元,则至少购进![]() 型车多少辆?
型车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.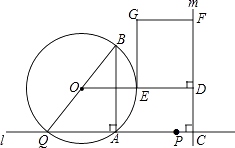
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
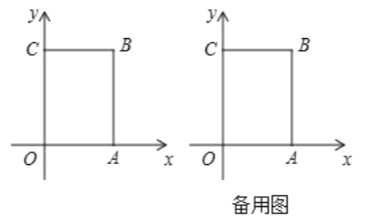
【题目】如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() 且
且![]() 满足
满足![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒
从原点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 的线路移动.
的线路移动.
![]() 求点
求点![]() 的坐标为 ;当点
的坐标为 ;当点![]() 移动
移动![]() 秒时,点
秒时,点![]() 的坐标为
的坐标为
![]() 在移动过程中,当点
在移动过程中,当点![]() 移动
移动![]() 秒时,求
秒时,求![]() 的面积.
的面积.
![]() 在
在![]() 的条件下,坐标轴上是否存在点
的条件下,坐标轴上是否存在点![]() ,使
,使![]() 的面积与
的面积与![]() 的面积相等,若存在,求点
的面积相等,若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
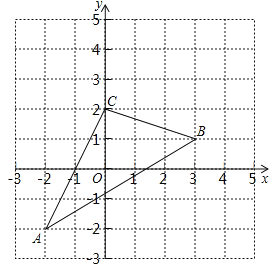
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向左平移1个单位得到△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )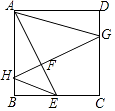
A.8
B.4 ![]()
C.2 ![]()
D.8 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
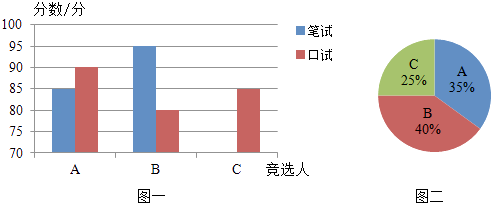
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com