
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
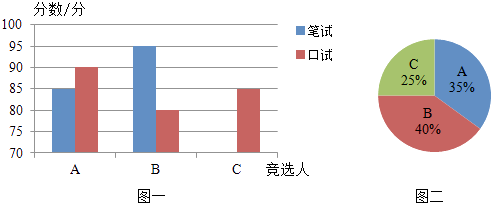
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
【答案】
(1)解:A大学生的口试成绩为90;补充后的图如图所示:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 90 | 80 | 85 |
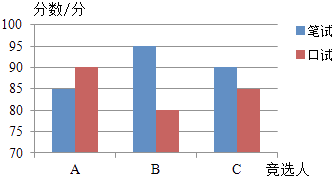
(2)解:A的票数为300×35%=105(张),
B的票数为300×40%=120(张),
C的票数为300×25%=75(张)
(3)解:A的成绩为 ![]() =92.5(分)
=92.5(分)
B的成绩为 ![]() =98(分)
=98(分)
C的成绩为 ![]() =84(分)
=84(分)
故B学生成绩最高,能当选学生会主席.
【解析】(1)结合表一和图一可以看出:A大学生的口试成绩为90分,再补充后的图即可;(2)根据总人数乘以A、B、C、的得票的百分数,即可得到每个人的得票数;(3)分别通过加权平均数的计算方法:即笔试![]() 权重1+口试
权重1+口试![]() 权重2,计算A的成绩,B的成绩,C的成绩,综合三人的得分,故B学生成绩最高,能当选学生会主席.
权重2,计算A的成绩,B的成绩,C的成绩,综合三人的得分,故B学生成绩最高,能当选学生会主席.


科目:初中数学 来源: 题型:
【题目】下列命题中,真命题有( )
①直线外一点与直线上各点连接的所有线段中,垂线段最短;
②三角形的一个外角大于任何一个内角;
③如果∠1和∠2是对顶角,那么![]() ;
;
④如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2015,则m的值是( )
A.43B.44C.45D.46
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )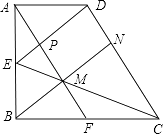
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距300千米的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.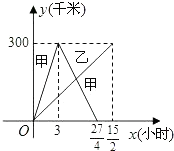
(1)请直接写出甲、乙两车离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并标明自变量x的取值范围;
(2)它们在行驶的过程中有几次相遇?并求出每次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足 ![]() +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树![]() 他先让爸爸开车驶过这段公路,发现速度为60千米
他先让爸爸开车驶过这段公路,发现速度为60千米![]() 小时,走了约3分钟,由此估算这段路长约______千米.
小时,走了约3分钟,由此估算这段路长约______千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米![]() 小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵数,请你求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.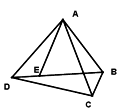
①试说明BE·AD=CD·AE;
②根据图形特点,猜想 ![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com