
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E,F分别是AB,BC边的中点,连接AF,CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )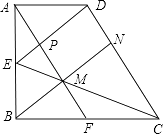
A.5个
B.4个
C.3个
D.2个
【答案】B
【解析】连接DF,AC,EF,如图所示:
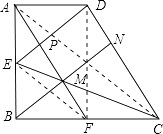
∵E、F分别为AB、BC的中点,且AB=BC,
∴AE=EB=BF=FC,
在△ABF和△CBE中,
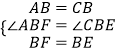 ,
,
∴△ABF≌△CBE(SAS),
∴∠BAF=∠BCE,AF=CE,
在△AME和△CMF中,
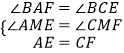 ,
,
∴△AME≌△CMF(AAS),
∴EM=FM,
在△BEM和△BFM中,
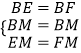 ,
,
∴△BEM≌△BFM(SSS),
∴∠ABN=∠CBN,选项①正确;
∵AE=AD,∠EAD=90°,
∴△AED为等腰直角三角形,
∴∠AED=45°,
∵∠ABC=90°,
∴∠ABN=∠CBN=45°,
∴∠AED=∠ABN=45°,
∴ED∥BN,选项②正确;
∵AB=BC=2AD,且BC=2FC,
∴AD=FC,又AD∥FC,
∴四边形AFCD为平行四边形,
∴AF=DC,又AF=CE,
∴DC=EC,
则△CED为等腰三角形,选项③正确;
∵EF为△ABC的中位线,
∴EF∥AC,且EF= ![]() AC,
AC,
∴∠MEF=∠MCA,∠EFM=∠MAC,
∴△EFM∽△CAM,
∴EM:MC=EF:AC=1:2,
设EM=x,则有MC=2x,EC=EM+MC=3x,
设EB=y,则有BC=2y,
在Rt△EBC中,根据勾股定理得:EC= ![]() =
= ![]() y,
y,
∴3x= ![]() y,即x:y=
y,即x:y= ![]() :3,
:3,
∴EM:BE= ![]() :3,选项④正确;
:3,选项④正确;
∵E为AB的中点,EP∥BM,
∴P为AM的中点,
∴S△AEP=S△EPM= ![]() S△AEM,
S△AEM,
又S△AEM=S△BEM,且S△BEM=S△BFM,
∴S△AEM=S△BEM=S△BFM= ![]() S△ABF,
S△ABF,
∵四边形ABFD为矩形,
∴S△ABF=S△ADF,又S△ADF=S△DFC,
∴S△ABF=S△ADF=S△DFC= ![]() S梯形ABCD,
S梯形ABCD,
∴S△EPM= ![]() S梯形ABCD,选项⑤错误.
S梯形ABCD,选项⑤错误.
则正确的个数有4个.
故答案为:B.
连接DF,AC,EF,如图所示,由E、F分别为AB、BC的中点,且AB=BC,得到EB=FB,再由一对公共角相等,利用“SAS”可得出△ABF与△CBE全等,利用AAS可得出△AME与△CMF全等,由全等三角形的对应边相等可得出ME=MF,再由BE=BF,BM=BM,利用SSS得到△BEM与△BFM全等,根据全等三角形的对应角相等可得出∠ABN=∠CBN,选项①正确;由AD=AE,梯形为直角梯形,得到∠EAD为直角,可得出△AED为等腰直角三角形,可得出∠AED为45°,由∠ABC为直角,且∠ABN=∠CBN,可得出∠ABN为45°,根据同位角相等可得出DE平行于BN,选项②正确;先得到AD=FC,又AD与FC平行,得到ADCF为平行四边形,可得出AF=DC,又AF=CE,等量代换可得出DC=EC,即△DCE为等腰三角形,选项③正确;由EF为△ABC的中位线,得出△EFM与△ACM相似,进而可得出EM:MC=1:2,设EM=x,则有MC=2x,用EM+MC表示出EC,设EB=y,根据BC=2EB,表示出BC,在直角三角形BCE中,利用勾股定理表示出EC,两者相等得到x与y的比值,即为EM与BE的比值,即可判断选项④正确与否;由E为AB的中点,利用等底同高得到△AME的面积与△BME的面积相等,由△BME与△BFM全等,得到面积相等,可得出三个三角形的面积相等都为△ABF面积的![]() ,进一步可得出△AEP的面积等于△PEM的面积,得到△PEM的面积为△ABF面积的
,进一步可得出△AEP的面积等于△PEM的面积,得到△PEM的面积为△ABF面积的![]() ,由ABFD为矩形得到△ABF与△ADF全等,面积相等,由△ADF与△CFD全等得到面积相等,可得出三个三角形面积相等都为梯形面积的
,由ABFD为矩形得到△ABF与△ADF全等,面积相等,由△ADF与△CFD全等得到面积相等,可得出三个三角形面积相等都为梯形面积的![]() ,综上得到△PEM的面积为梯形面积的
,综上得到△PEM的面积为梯形面积的![]() ,可得出选项⑤错误,综上,即可得到所求正确的个数.
,可得出选项⑤错误,综上,即可得到所求正确的个数.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
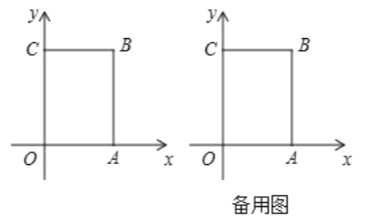
【题目】如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() 且
且![]() 满足
满足![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒
从原点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 的线路移动.
的线路移动.
![]() 求点
求点![]() 的坐标为 ;当点
的坐标为 ;当点![]() 移动
移动![]() 秒时,点
秒时,点![]() 的坐标为
的坐标为
![]() 在移动过程中,当点
在移动过程中,当点![]() 移动
移动![]() 秒时,求
秒时,求![]() 的面积.
的面积.
![]() 在
在![]() 的条件下,坐标轴上是否存在点
的条件下,坐标轴上是否存在点![]() ,使
,使![]() 的面积与
的面积与![]() 的面积相等,若存在,求点
的面积相等,若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.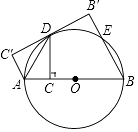
(1)请你判断C′D与⊙O的位置关系,并说明理由;
(2)过点B作BB′⊥C′D′于B′,交⊙O于E,若CD= ![]() ,AC=3,求BE的长.
,AC=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 在边
在边![]() 上,且
上,且![]() .
.

(1)如图![]() ,当
,当![]() 时,将
时,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() 的位置,连接
的位置,连接![]() ,
,
①求![]() 的度数;
的度数;
②求证:![]() ;
;
(2)如图![]() ,当
,当![]() 时,猜想
时,猜想![]() 、
、![]() 、
、![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图![]() ,当
,当![]() ,
,![]() ,
,![]() 时,请直接写出
时,请直接写出![]() 的长为________.
的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
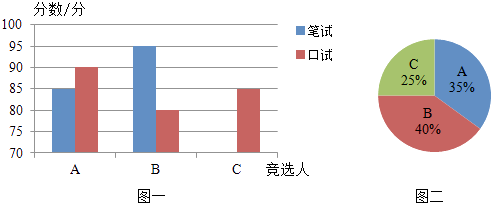
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.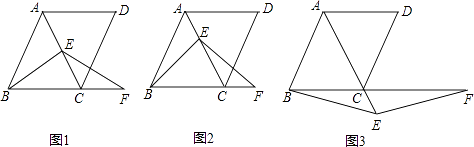
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点(点
两点(点 ![]() 在点
在点 ![]() 的左侧),点
的左侧),点 ![]() 的坐标为
的坐标为 ![]() ,与
,与 ![]() 轴交于点
轴交于点 ![]() ,作直线
,作直线 ![]() .动点
.动点 ![]() 在
在 ![]() 轴上运动,过点
轴上运动,过点 ![]() 作
作 ![]() 轴,交抛物线于点
轴,交抛物线于点 ![]() ,交直线
,交直线 ![]() 于点
于点 ![]() ,设点
,设点 ![]() 的横坐标为
的横坐标为 ![]() .
.
(Ⅰ)求抛物线的解析式和直线 ![]() 的解析式;
的解析式;
(Ⅱ)当点 ![]() 在线段
在线段 ![]() 上运动时,求线段
上运动时,求线段 ![]() 的最大值;
的最大值;
(Ⅲ)当以 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.如果∠BAC=30°,∠DAE=105°,则y与x之间的函数关系式为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com